【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若![]() 在
在![]() 上是单调增函数,求实数
上是单调增函数,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)求出函数的定义域以及导数,结合定义域,讨论![]() 和
和![]() 情况下,导数的正负,即可得到
情况下,导数的正负,即可得到![]() 的单调性;
的单调性;
(2)求出![]() ,则
,则![]() 在
在![]() 上是单调增函数等价于
上是单调增函数等价于![]() 在
在![]() 上恒成立,分离参数
上恒成立,分离参数![]() ,即
,即![]() 在
在![]() 恒成立,令
恒成立,令![]() ,
,
利用导数求出函数![]() 在
在![]() 上的最大值,即可得到实数
上的最大值,即可得到实数![]() 的取值范围
的取值范围
(1)函数![]() ,则函数
,则函数![]() 的定义域为
的定义域为![]() .
.
![]()
①当![]() 时,
时,![]() 故函数
故函数![]() 在
在![]() 上单调递增;
上单调递增;
②当![]() 时,在
时,在 有
有![]() 故
故![]() 在
在![]() 单调递减;
单调递减;
在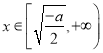 有
有![]() 故
故![]() 在
在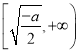 上单调递增。
上单调递增。
综上所述:当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,函数
时,函数![]() 在
在![]() 上为单调递减,在
上为单调递减,在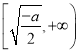 上为单调递减增
上为单调递减增
(2)由![]() ,得
,得![]() .
.
若函数![]() 为
为![]() 上的单调增函数,则
上的单调增函数,则![]() 在
在![]() 上恒成立,
上恒成立,
即不等式![]() 在
在![]() 上恒成立.也即
上恒成立.也即![]() 在
在![]() 上恒成立.
上恒成立.
令![]() ,则
,则![]() .
.
当![]() 时,
时,![]() ,
,
![]()
![]() 在
在![]() 上为减函数,则
上为减函数,则![]()
所以![]() ,即
,即![]() 的取值范围为
的取值范围为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一枚质地均匀的硬币连掷
 次,设事件
次,设事件 “恰好两次正面朝上”,
“恰好两次正面朝上”,(1)直接计算事件
 的概率;
的概率;(2)利用计算器或计算机模拟试验80次,计算事件
 发生的频率.
发生的频率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,函数
,函数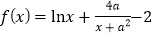 .
.(1)记
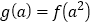 ,求
,求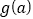 的最小值;
的最小值;(2)若
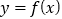 有三个不同的零点,求
有三个不同的零点,求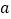 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,
中, 比
比 长4,
长4, 比
比 长2,且最大角的余弦值是
长2,且最大角的余弦值是 ,则
,则 的面积等于______________.
的面积等于______________. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个正方体的平面展开图及该正方体的直观图的示意图如图所示.
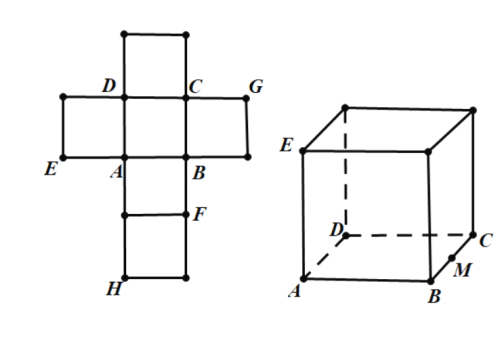
(Ⅰ)请按字母F,G,H标记在正方体相应地顶点处(不需要说明理由)
(Ⅱ)判断平面BEG与平面ACH的位置关系.并说明你的结论.
(Ⅲ)证明:直线DF
 平面BEG
平面BEG -
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)已知椭圆
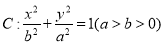 的离心率为
的离心率为 ,椭圆C的长轴长为4.
,椭圆C的长轴长为4.(1)求椭圆C的方程;
(2)已知直线
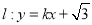 与椭圆C交于A,B两点,是否存在实数k使得以线段AB 为直径的圆恰好经过坐标原点O?若存在,求出k的值;若不存在,请说明理由.
与椭圆C交于A,B两点,是否存在实数k使得以线段AB 为直径的圆恰好经过坐标原点O?若存在,求出k的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
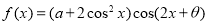 为奇函数,且
为奇函数,且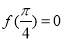 ,其中
,其中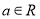 ,
,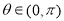 .
.(1)求
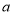 ,
,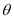 的值.
的值.(2)若
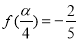 ,
,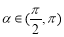 ,求
,求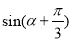 的值.
的值.
相关试题

