【题目】(2016·全国Ⅲ卷)已知数列{an}的前n项和Sn=1+λan,其中λ≠0.
(1)证明{an}是等比数列,并求其通项公式;
(2)若S5=![]() ,求λ.
,求λ.
参考答案:
【答案】(1)见解析(2)λ=-1.
【解析】试题分析:(1)利用前n项和与前n-1项和相减,即可得出数列的通项公式。
(2)通过等比数列前n项和公式,以及前5项和的值列出方程,即可求出等比数列的公比。
试题解析:(1)证明 由题意得a1=S1=1+λa1,故λ≠1,a1=![]() ,a1≠0.
,a1≠0.
由Sn=1+λan,Sn+1=1+λan+1,
得an+1=λan+1-λan,
即an+1(λ-1)=λan,由a1≠0,λ≠0得an≠0,
所以![]() =
=![]() .
.
因此{an}是首项为![]() ,公比为
,公比为![]() 的等比数列,
的等比数列,
于是an=![]()
![]()
![]() .
.
(2)解 由(1)得Sn=1-![]()
![]() .
.
由S5=![]() 得1-
得1-![]() =
=![]() ,即
,即![]() =
=![]() .
.
解得λ=-1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知复数z=bi(b∈R),
 是纯虚数,i是虚数单位.
是纯虚数,i是虚数单位.(1)求复数z;
(2)若复数(m+z)2所表示的点在第二象限,求实数m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于数集
 ,其中
,其中 ,
,  ,定义向量集
,定义向量集 .若对于任意
.若对于任意 ,使得
,使得 ,则称
,则称 具有性质
具有性质 .例如
.例如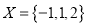 具有性质
具有性质 .
.(
 )若
)若 ,且
,且 具有性质
具有性质 ,求
,求 的值.
的值.(
 )若
)若 具有性质
具有性质 ,求证:
,求证:  ,且当
,且当 时,
时,  .
.(
 )若
)若 具有性质
具有性质 ,且
,且 ,
,  (
( 为常数),求有穷数列
为常数),求有穷数列 ,
,  ,
,  ,
,  的通项公式.
的通项公式. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个正方体图形中,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,能得出AB∥平面MNP的图形的个数有( )

A.1B.2C.3D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,梯形ABCD中,AD∥BC,AD=AB=1,AD⊥AB,∠BCD=45°,将△ABD沿对角线BD折起,设折起后点A的位置为A′,使二面角A′—BD—C为直二面角,给出下面四个命题:①A′D⊥BC;②三棱锥A′—BCD的体积为
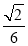 ;③CD⊥平面A′BD;④平面A′BC⊥平面A′DC.其中正确命题的个数是( )
;③CD⊥平面A′BD;④平面A′BC⊥平面A′DC.其中正确命题的个数是( )
A.1B.2C.3D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}满足a1=1,an+1=3an+1.
(1)证明
 是等比数列,并求{an}的通项公式;
是等比数列,并求{an}的通项公式;(2)证明:
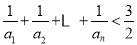 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
 =(-2,1),
=(-2,1), =(x,y).
=(x,y).(1)若x,y分别表示将一枚质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次时第一次、第二次出现的点数,求满足
 的概率;
的概率;(2)若x,y在区间[1,6]内取值,求满足
 的概率.
的概率.
相关试题

