【题目】已知函数f(x)=x﹣lnx+a﹣1,g(x)= ![]() +ax﹣xlnx,其中a>0.
+ax﹣xlnx,其中a>0.
(1)求f(x)的单调区间;
(2)当x≥1时,g(x)的最小值大于 ![]() ﹣lna,求a的取值范围.
﹣lna,求a的取值范围.
参考答案:
【答案】
(1)解:函数f(x)的定义域为(0,+∞).,
![]()
当0<x<1时,f'(x)<0;当x>1时,f'(x)>0.
∴函数f(x)的单调递减区间是(0,1),单调递增区间是(1,+∞)
(2)解:易知g'(x)=x﹣lnx+a﹣1=f(x).
由(1)知,f(x)≥f(1)=a>0,
所以当x≥1时,g'(x)≥g'(1)=a>0.
从而g(x)在[1,+∞)上单调递增,
所以g(x)的最小值 ![]() .
.
依题意得 ![]() ,即a+lna﹣1>0.
,即a+lna﹣1>0.
令h(a)=lna+a﹣1,易知h(a)在(0,+∞)上单调递增.
所以h(a)>h(1)=0,所以a的取值范围是(1,+∞)
【解析】(1)求出函数的导数,利用导数的符号求解函数的单调性.(2)利用g'(x)=x﹣lnx+a﹣1=f(x).结合(1)知,判断g(x)在[1,+∞)上单调递增,求出g(x)的最小值,推出a+lna﹣1>0,令h(a)=lna+a﹣1,利用h(a)在(0,+∞)上单调递增.求解a的范围.
【考点精析】通过灵活运用利用导数研究函数的单调性,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减即可以解答此题.
在这个区间单调递减即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2019年4月20日,福建省人民政府公布了“3+1+2”新高考方案,方案中“2”指的是在思想政治、地理、化学、生物4门中选择2门.“2”中记入高考总分的单科成绩是由原始分转化得到的等级分,学科高考原始分在全省的排名越靠前,等级分越高小明同学是2018级的高一学生.已确定了必选地理且不选政治,为确定另选一科,小明收集并整理了化学与生物近10大联考的成绩百分比排名数据x(如x=19的含义是指在该次考试中,成绩高于小明的考生占参加该次考试的考生数的19%)绘制茎叶图如下.

(1)分别计算化学、生物两个学科10次联考的百分比排名的平均数;中位数;
(2)根据已学的统计知识,并结合上面的数据,帮助小明作出选择.并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】据相关规定,24小时内的降水量为日降水量(单位:mm),不同的日降水量对应的降水强度如表:
日降水量
(0,10)
[10,25)
[25,50)
[50,100)
[100,250)
[250,+∞)
降水强度
小雨
中雨
大雨
暴雨
大暴雨
特大暴雨
为分析某市“主汛期”的降水情况,从该市2015年6月~8月有降水记录的监测数据中,随机抽取10天的数据作为样本,具体数据如下:
16 12 23 65 24 37 39 21 36 68
(1)请完成以如表示这组数据的茎叶图;
(2)从样本中降水强度为大雨以上(含大雨)天气的5天中随机选取2天,求恰有1天是暴雨天气的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知定圆
 :
: ,动圆
,动圆 过点
过点
 且与圆
且与圆 相切,记圆心
相切,记圆心 的轨迹为
的轨迹为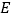 .
.(1)求曲线
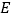 的方程;
的方程;(2)已知直线

 交圆
交圆 于
于 两点.
两点. 是曲线
是曲线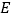 上两点,若四边形
上两点,若四边形 的对角线
的对角线 ,求四边形
,求四边形 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】土笋冻是闽南种广受欢迎的特色传统风味小吃某小区超市销售一款土笋冻,进价为每个15元,售价为每个20元.销售的方案是当天进货,当天销售,未售出的全部由厂家以每个10元的价格回购处理.根据该小区以往的销售情况,得到如图所示的频率分布直方图:

(1)估算该小区土笋冻日需求量的平均数
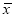 (同一组中的数据用该组区间的中点值代表);
(同一组中的数据用该组区间的中点值代表);(2)已知该超市某天购进了150个土笋冻,假设当天的需求量为
 个
个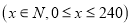 销售利润为
销售利润为 元.
元.(i)求关于
 的函数关系式;
的函数关系式;(ii)结合上述频率分布直方图,以额率估计概率的思想,估计当天利润
 不小于650元的概率.
不小于650元的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)讨论
 的单调性;
的单调性;(2)当
 时,
时, ,求
,求 的最大整数值.
的最大整数值. -
科目: 来源: 题型:
查看答案和解析>>【题目】[选修4-4:坐标系与参数方程]
在直角坐标系
 中,曲线
中,曲线 的参数方程为
的参数方程为 (
( 为参数),以原点
为参数),以原点 为极点,
为极点,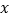 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.(1)求曲线
 的极坐标方程;
的极坐标方程;(2)若点
 的极坐标为
的极坐标为 ,
, 是曲线
是曲线 上的一动点,求
上的一动点,求 面积的最大值.
面积的最大值.
相关试题

