【题目】(1)已知函数y=lg(x2+2x+a)的定义域为R,求实数a的取值范围;
(2)已知函数f(x)=lg[(a2-1)x2+(2a+1)x+1],若f(x)的定义域为R,求实数a的取值范围.
参考答案:
【答案】(1)(1,+∞);(2)(-∞,-![]() ).
).
【解析】试题分析:(1)由题意得一元二次不等式恒成立,再根据二次函数图像得判别式小于零(2)由题意得不等式恒成立,再分类讨论一次与二次函数,最后根据二次函数图像得判别式小于零
试题解析:(1)因为y=lg(x2+2x+a)的定义域为R,
所以x2+2x+a>0恒成立,所以Δ=4-4a<0,
所以 a>1.
故a的取值范围是(1,+∞).
(2)依题意(a2-1)x2+(2a+1)x+1>0对一切x∈R恒成立.
当a2-1≠0时,![]()
解得a<-![]() .
.
当a2-1=0时,显然(2a+1)x+1>0,对x∈R不恒成立.
所以a的取值范围是(-∞,-![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形
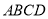 中,
中, 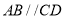 ,
,  ,
, 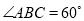 ,四边形
,四边形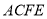 为矩形,平面
为矩形,平面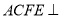 平面
平面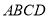 ,
, 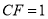 .
.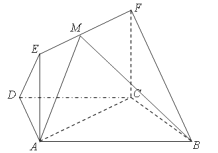
(1)求证:
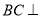 平面
平面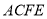 ;
;(2)点
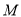 在线段
在线段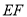 上运动,设平面
上运动,设平面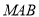 与平面
与平面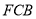 所成二面角的平面角为
所成二面角的平面角为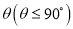 ,试求
,试求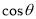 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形物体E在雨中沿面P(面积为S)的垂直方向作匀速移动,速度为
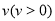 ,雨速沿E移动方向的分速度为
,雨速沿E移动方向的分速度为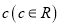 。E移动时单位时间内的淋雨量包括两部分:(1)P或P的平行面(只有一个面淋雨)的淋雨量,假设其值与
。E移动时单位时间内的淋雨量包括两部分:(1)P或P的平行面(只有一个面淋雨)的淋雨量,假设其值与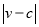 ×S成正比,比例系数为
×S成正比,比例系数为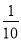 ;(2)其它面的淋雨量之和,其值为
;(2)其它面的淋雨量之和,其值为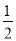 ,记
,记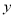 为E移动过程中的总淋雨量,当移动距离d=100,面积S=
为E移动过程中的总淋雨量,当移动距离d=100,面积S=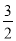 时。
时。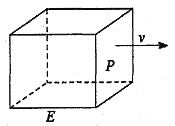
(1)写出
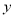 的表达式
的表达式(2)设0<v≤10,0<c≤5,试根据c的不同取值范围,确定移动速度
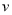 ,使总淋雨量
,使总淋雨量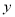 最少。
最少。 -
科目: 来源: 题型:
查看答案和解析>>【题目】5名男生4名女生站成一排,求满足下列条件的排法:
(1)女生都不相邻有多少种排法?
(2)男生甲、乙、丙排序一定(只考虑位置的前后顺序),有多少种排法?
(3)男甲不在首位,男乙不在末位,有多少种排法?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=2sin(x-
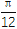 )-
)-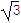 ,现将f(x)的图象向左平移
,现将f(x)的图象向左平移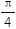 个单位长度,再向上平移
个单位长度,再向上平移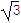 个单位长度,得到函数g(x)的图象.
个单位长度,得到函数g(x)的图象.(1)求f(
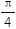 )+g(
)+g(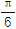 )的值;
)的值;(2)若a,b,c分别是△ABC三个内角A,B,C的对边,a+c=4,且当x=B时,g(x)取得最大值,求b的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 sinωx·cosωx-cos2ωx(ω>0)的最小正周期为
sinωx·cosωx-cos2ωx(ω>0)的最小正周期为 .
.(1)求ω的值;
(2)在△ABC中,sinB,sinA,sinC成等比数列,求此时f(A)的值域.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数
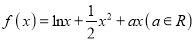 ,
, 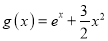 .
.(Ⅰ)讨论
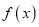 的极值点的个数;
的极值点的个数;(Ⅱ)若对于任意
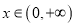 ,总有
,总有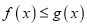 成立,求实数
成立,求实数 的取值范围.
的取值范围.
相关试题

