【题目】已知函数![]() .
.
(1)求函数![]() 的图象在
的图象在![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 在
在![]() 上有两个不同的零点,求实数
上有两个不同的零点,求实数![]() 的取值范围;
的取值范围;
(3)是否存在实数![]() ,使得对任意的
,使得对任意的![]() ,都有函数
,都有函数![]() 的图象在
的图象在![]() 的图象的下方?若存在,请求出最大整数
的图象的下方?若存在,请求出最大整数![]() 的值;若不存在,请说理由.
的值;若不存在,请说理由.
(参考数据: ![]() ,
, ![]() ).
).
参考答案:
【答案】(1)![]() (2)
(2)![]() (3)最大整数
(3)最大整数![]() 的值为
的值为![]() .
.
【解析】试题分析:(1)求函数的导数,利用导数的几何意义进行求解;(2)利用参数分离法![]() ,转化为两个函数有两个不同的交点即可;(3)
,转化为两个函数有两个不同的交点即可;(3)![]() 的图象在
的图象在![]() 的图象的下方,等价为对任意的
的图象的下方,等价为对任意的![]() ,
, ![]() 恒成立,利用参数分离法,结合函数的单调性和导数之间的关系进行期间即可.
恒成立,利用参数分离法,结合函数的单调性和导数之间的关系进行期间即可.
试题解析:(1)因为![]() ,所以
,所以![]() ,则所求切线的斜率为
,则所求切线的斜率为![]() ,
,
又![]() ,故所求切线的方程为
,故所求切线的方程为![]() .
.
(2)因为![]() ,则由题意知方程
,则由题意知方程![]() 在
在![]() 上有两个不同的根.
上有两个不同的根.
由![]() ,得
,得![]() ,
,
令![]() ,则
,则![]() ,由
,由![]() ,解得
,解得![]() .
.
当![]() 时,
时, ![]() ,
, ![]() 单调递减;当
单调递减;当![]() 时,
时, ![]() ,
, ![]() 单调递增,
单调递增,
所以当![]() 时,
时, ![]() 取得最小值为
取得最小值为![]() .
.
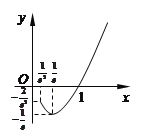
又![]() ,
, ![]() (图象如右图所示),
(图象如右图所示),
所以![]() ,解得
,解得![]() .
.
(3)假设存在实数![]() 满足题意,则不等式
满足题意,则不等式![]() 对
对![]() 恒成立.
恒成立.
即![]() 对
对![]() 恒成立.
恒成立.
令![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() ,
,
因为![]() 在
在![]() 上单调递增,
上单调递增, ![]() ,
, ![]() ,且
,且![]() 的图象在
的图象在![]() 上不间断,所以存在
上不间断,所以存在,使得
![]() ,即
,即![]() ,则
,则![]() ,
,
所以当![]() 时,
时, ![]() 单调递减;当
单调递减;当![]() 时,
时, ![]() 单调递增,
单调递增,
则![]() 取到最小值
取到最小值![]()
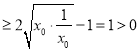 ,…14分
,…14分
所以![]() ,即
,即![]() 在区间
在区间![]() 内单调递增.
内单调递增.
所以![]() ,
,
所以存在实数![]() 满足题意,且最大整数
满足题意,且最大整数![]() 的值为
的值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】等比数列{an}的前n项和为Sn,已知对任意的n∈N*,点(n,Sn)均在函数y=bx+r(b>0且b≠1,b,r均为常数)的图象上.
(1)求r的值;
(2)当b=2时,记bn=2(log2an+1)(n∈N*),证明:对任意的n∈N*,不等式
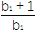 ·
·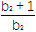 ·…·
·…· >
> 成立.
成立. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2-ax+ln(x+1)(a∈R).
(1)当a=2时,求函数f(x)的极值点;
(2)若函数f(x)在区间(0,1)上恒有f′(x)>x,求实数a的取值范围;
(3)已知a<1,c1>0,且cn+1=f′(cn)(n=1,2,…),证明数列{cn}是单调递增数列.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=aln x+
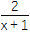 (a∈R).
(a∈R).(1)当a=1时,求f(x)在x∈[1,+∞)内的最小值;
(2)若f(x)存在单调递减区间,求a的取值范围;
(3)求证ln(n+1)>
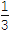 +
+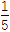 +
+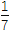 +…+
+…+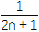 (n∈N*).
(n∈N*). -
科目: 来源: 题型:
查看答案和解析>>【题目】有一个食品商店为了调查气温对热饮销售的影响,经过调查得到关于卖出的热饮杯数与当天气温的数据如下表,绘出散点图如下.通过计算,可以得到对应的回归方程
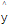 =-2.352x+147.767,根据以上信息,判断下列结论中正确的是( )
=-2.352x+147.767,根据以上信息,判断下列结论中正确的是( )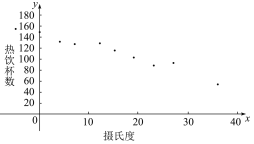
摄氏温度
-5
0
4
7
12
15
19
23
27
31
36
热饮杯数
156
150
132
128
130
116
104
89
93
76
54
A.气温与热饮的销售杯数之间成正相关
B.当天气温为2℃时,这天大约可以卖出143杯热饮
C.当天气温为10℃时,这天恰卖出124杯热饮
D.由于x=0时,
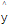 的值与调查数据不符,故气温与卖出热饮杯数不存在线性相关性
的值与调查数据不符,故气温与卖出热饮杯数不存在线性相关性 -
科目: 来源: 题型:
查看答案和解析>>【题目】某制药厂生产某种颗粒状粉剂,由医药代表负责推销,若每包药品的生产成本为
 元,推销费用为
元,推销费用为 元,预计当每包药品销售价为
元,预计当每包药品销售价为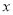 元时,一年的市场销售量为
元时,一年的市场销售量为 万包,若从民生考虑,每包药品的售价不得高于生产成本的
万包,若从民生考虑,每包药品的售价不得高于生产成本的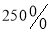 ,但为了鼓励药品研发,每包药品的售价又不得低于生产成本的
,但为了鼓励药品研发,每包药品的售价又不得低于生产成本的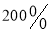
(1) 写出该药品一年的利润
 (万元)与每包售价
(万元)与每包售价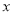 的函数关系式,并指出其定义域;
的函数关系式,并指出其定义域;(2) 当每包药品售价
 为多少元时,年利润
为多少元时,年利润 最大,最大值为多少?
最大,最大值为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】一次猜奖游戏中,1,2,3,4四扇门里摆放了
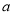 ,
, 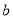 ,
, 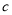 ,
, 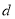 四件奖品(每扇门里仅放一件).甲同学说:1号门里是
四件奖品(每扇门里仅放一件).甲同学说:1号门里是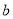 ,3号门里是
,3号门里是 ;乙同学说:2号门里是
;乙同学说:2号门里是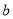 ,3号门里是
,3号门里是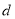 ;丙同学说:4号门里是
;丙同学说:4号门里是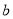 ,2号门里是
,2号门里是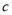 ;丁同学说:4号门里是
;丁同学说:4号门里是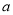 ,3号门里是
,3号门里是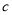 .如果他们每人都猜对了一半,那么4号门里是( )
.如果他们每人都猜对了一半,那么4号门里是( )A.
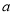 B.
B. 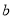 C.
C. 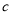 D.
D. 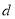
相关试题

