【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)若![]() ,求
,求![]() 的极值;
的极值;
(Ⅱ)若对于任意的![]() ,
,![]() ,都有
,都有![]() ,求
,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(Ⅰ)![]() 有极小值
有极小值![]() ,没有极大值;(Ⅱ)
,没有极大值;(Ⅱ)![]() .
.
【解析】
试题分析:(Ⅰ)将![]() 代入函数
代入函数![]() 的表达式,求出
的表达式,求出![]() 的导数,得到函数的单调区间,从而求出函数的极值即可;(Ⅱ)对于任意的
的导数,得到函数的单调区间,从而求出函数的极值即可;(Ⅱ)对于任意的![]() ,
,![]() 有
有![]() ,
,![]() .所以有
.所以有![]() 恒成立,即
恒成立,即![]() ,构造函数
,构造函数![]() ,利用导数求
,利用导数求![]() 最大值
最大值![]() ,只需
,只需![]() 即可.
即可.
试题解析:(Ⅰ)![]() 的定义域为
的定义域为![]() ,
,![]() 时,
时,
![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() 是增函数,
是增函数,![]() ,
,![]() ,
,![]() 是减函数.
是减函数.
∴![]() 有极小值
有极小值![]() ,没有极大值.………………………5分
,没有极大值.………………………5分
(Ⅱ)![]() ,
,![]()
当![]() 时,
时,![]() ,∴
,∴![]() 在
在![]() 上是单调递增函数,
上是单调递增函数,![]() 最大,………………7分
最大,………………7分
对于任意的![]() ,
,![]() .
.
![]() 恒成立,即对任意
恒成立,即对任意![]() ,
,![]() 恒成立,∴
恒成立,∴![]() ,…………9分
,…………9分
令![]() ,则
,则![]() .
.
∴当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数,
上是减函数,
当![]() 时,
时,![]() 最大值为
最大值为![]() ,…………………………11分
,…………………………11分
∴![]() 即
即![]() .……………………12分
.……………………12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】某理科考生参加自主招生面试,从7道题中(4道理科题3道文科题)不放回地依次任取3道作答.
(1)求该考生在第一次抽到理科题的条件下,第二次和第三次均抽到文科题的概率;
(2)规定理科考生需作答两道理科题和一道文科题,该考生答对理科题的概率均为
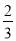 ,答对文科题的概率均为
,答对文科题的概率均为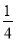 ,若每题答对得10分,否则得零分.现该生已抽到三道题(两理一文),求其所得总分
,若每题答对得10分,否则得零分.现该生已抽到三道题(两理一文),求其所得总分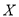 的分布列与数学期望
的分布列与数学期望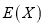 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知全集U=R,A={x|x2﹣2x﹣3≤0},B={x|2≤x<5},C={x|x>a}.
(1)求A∩(UB);
(2)若A∪C=C,求a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,海上有
 、
、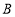 两个小岛相距
两个小岛相距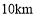 ,船
,船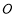 将保持观望
将保持观望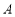 岛和
岛和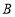 岛所成的视角为
岛所成的视角为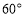 ,现从船
,现从船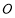 上派下一只小艇沿
上派下一只小艇沿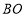 方向驶至
方向驶至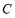 处进行作业,且
处进行作业,且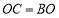 .设
.设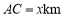 .
.
(1)用
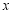 分别表示
分别表示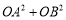 和
和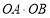 ,并求出
,并求出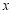 的取值范围;
的取值范围;(2)0晚上小艇在
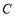 处发出一道强烈的光线照射
处发出一道强烈的光线照射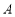 岛,
岛,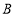 岛至光线
岛至光线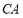 的距离为
的距离为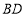 ,求
,求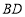 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为招聘新员工设计了一个面试方案:应聘者从6道备选题中一次性随机抽取3道题,按题目要求独立完成.规定:至少正确完成其中2道题的便可通过.已知6道备选题中应聘者甲有4道题能正确完成,2道题不能完成;应聘者乙每题正确完成的概率都是
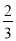 ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响.(1)分别求甲、乙两人正确完成面试题数的分布列及数学期望;
(2)请分析比较甲、乙两人谁面试通过的可能性大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的正方形中随机投掷10 000个点,则落入阴影部分(曲线C为正态分布
N(-1,1)的部分密度曲线)的点的个数的估计值为
附:若X~N(μ,σ2),则P(μ-σ<X<μ+σ)=0.682 6,P(μ-2σ<X<μ+2σ)=0.954 4.
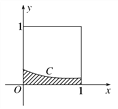
A. 1 193 B. 1 359 C. 2 718 D. 3 413
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
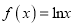 ,
, 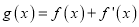
(Ⅰ)求
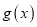 的单调区间和最小值;
的单调区间和最小值;(Ⅱ)讨论
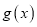 与
与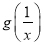 的大小关系;
的大小关系;(Ⅲ)求
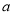 的取值范围,使得
的取值范围,使得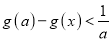 对任意
对任意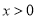 成立.
成立.
相关试题

