【题目】已知{an}是等差数列,{bn}是等比数列,且b2=3,b3=9,a1=b1,a14=b4.
(1)求{an}的通项公式;
(2)设cn=an+bn,求数列{cn}的前n项和.
参考答案:
【答案】见解析
【解析】解:(1)设等比数列{bn}的公比为q,
则q=![]() =
=![]() =3,
=3,
∴b1=![]() =1,b4=b3q=27,
=1,b4=b3q=27,
∴bn=3n-1(n=1,2,3,…).
设等差数列{an}的公差为d.
∵a1=b1=1,a14=b4=27,
∴1+13d=27,
即d=2.
∴an=2n-1(n=1,2,3,…).
(2)由(1)知an=2n-1,bn=3n-1,
因此cn=an+bn=2n-1+3n-1.
从而数列{cn}的前n项和
Sn=1+3+…+(2n-1)+1+3+…+3n-1=![]() +
+![]() =n2+
=n2+![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为确立下一年度投入某种产品的宣传费,需了解年宣传费
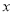 (单位:千元)对年销售量
(单位:千元)对年销售量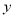 (单位:
(单位:  )和年利润
)和年利润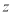 (单位:千元)的影响.对近
(单位:千元)的影响.对近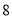 年的宣传费
年的宣传费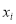 和年销售量
和年销售量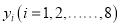 数据作了初步处理,得到下面的散点图及一些统计量的值.
数据作了初步处理,得到下面的散点图及一些统计量的值.表中
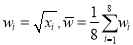

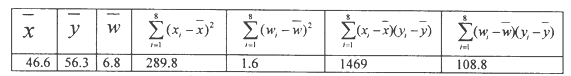
(Ⅰ)根据散点图判断,
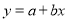 与
与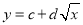 哪一个适宜作为年销售量
哪一个适宜作为年销售量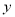 关于年宣传费
关于年宣传费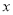 的回归方程类型?(给出判断即可,不必说明理由)
的回归方程类型?(给出判断即可,不必说明理由)(Ⅱ)根据(Ⅰ)的判断结果及表中数据,建立
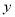 关于
关于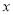 的回归方程;
的回归方程;(Ⅲ)已知这种产品的年利率
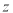 与
与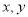 的关系为
的关系为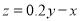 .根据(Ⅱ)的结果回答下列问题:
.根据(Ⅱ)的结果回答下列问题:(i)年宣传费
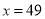 时,年销售量及利润的预报值是多少?
时,年销售量及利润的预报值是多少?(ii)年宣传费
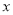 为何值时,年利率的预报值最大?
为何值时,年利率的预报值最大?附:对于一组数据
 ……
……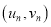 ,其回归线
,其回归线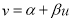 的斜率和截距的最小二乘法估计分别为:
的斜率和截距的最小二乘法估计分别为:  ,
, 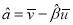
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱柱
 的底面是边长为2的正三角形且侧棱垂直于底面,侧棱长是
的底面是边长为2的正三角形且侧棱垂直于底面,侧棱长是 ,
,  是
是 的中点.
的中点.
(1)求证:
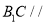 平面
平面 ;
;(2)求二面角
 的大小;
的大小;(3)求直线
 与平面
与平面 所成角的正弦值.
所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
 的首项
的首项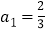 ,
, .
.(1)证明:数列
 是等比数列;
是等比数列;(2)求数列
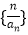 的前
的前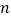 项和为
项和为 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如果函数
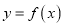 在定义域内给定区间
在定义域内给定区间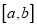 上存在
上存在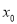 (
(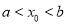 ),满足
),满足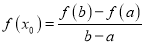 ,则称函数
,则称函数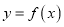 是
是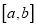 上的“平均值函数”,
上的“平均值函数”, 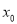 是它的一个均值点.如
是它的一个均值点.如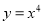 是
是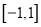 上的平均值函数,0就是他的均值点.
上的平均值函数,0就是他的均值点.(1)判断函数
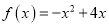 在区间
在区间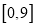 上是否为平均值函数?若是,求出它的均值点;若不是,请说明理由;
上是否为平均值函数?若是,求出它的均值点;若不是,请说明理由;(2)若函数
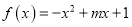 是区间
是区间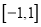 上的平均值函数,试确定实数
上的平均值函数,试确定实数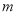 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
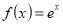 (
(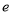 为自然对数的底数,
为自然对数的底数,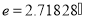 ),
),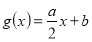 (
(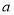 ,
,
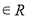 ),
),⑴若
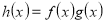 ,
,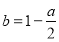 .求
.求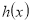 在
在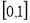 上的最大值
上的最大值 的表达式;
的表达式;⑵若
 时,方程
时,方程 在
在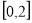 上恰有两个相异实根,求实根
上恰有两个相异实根,求实根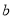 的取值范围;
的取值范围;⑶若
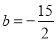 ,
, ,求使
,求使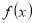 得图像恒在
得图像恒在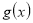 图像上方的最大正整数
图像上方的最大正整数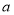 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合
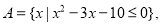 若
若(1)
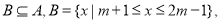 求实数
求实数 的范围;
的范围;(2)
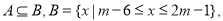 求实数
求实数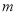 的范围;
的范围;(3)
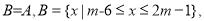 求实数
求实数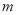 的范围.
的范围.
相关试题

