【题目】如图,在多面体ABCDE中,DB⊥平面ABC,AE∥DB,且△ABC为等边三角形,AE=1,BD=2,CD与平面ABCDE所成角的正弦值为 ![]() .
. 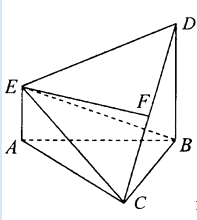
(1)若F是线段CD的中点,证明:EF⊥平面DBC;
(2)求二面角D﹣EC﹣B的平面角的余弦值.
参考答案:
【答案】
(1)证明:取BC的中点为M,连接FM,则可证AM⊥平面BCD,四边形AEFM为平行四边形,
所以EF∥AM,所以EF⊥平面DBC
(2)解:取AB的中点O,连结OC,OD,则OC⊥平面ABD,∠CDO即是CD与平面ABDE所成角, ![]() ,
,
设AB=x,则有 ![]() ,得AB=2,取DE的中点为G,
,得AB=2,取DE的中点为G,
以O为原点,OC为x轴,OB为y轴,OG为z轴,建立如图空间直角坐标系,则 ![]() ,
,
由(1)知:BF⊥平面DEC,又取平面DEC的一个法向量 ![]() =(
=( ![]() ,﹣1,2),
,﹣1,2),
设平面BCE的一个法向量 ![]() =(1,y,z),由,由此得平面BCE的一个法向量
=(1,y,z),由,由此得平面BCE的一个法向量 ![]() =(1,
=(1, ![]() ,2
,2 ![]() ),
),
则cos< ![]() ,
, ![]() >=
>= ![]() =
= ![]() =
= ![]() =
= ![]()
所以二面角D﹣EC﹣B的平面角的余弦值为 ![]()
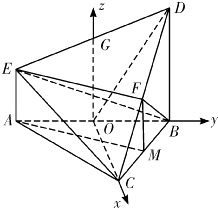
【解析】(1)根据线面垂直的判定定理进行证明即可.(2)建立坐标系,求出平面的法向量,利用向量法进行求解即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线方程为x2=2py(p>0),其焦点为F,点O为坐标原点,过焦点F作斜率为k(k≠0)的直线与抛物线交于A,B两点,过A,B两点分别作抛物线的两条切线,设两条切线交于点M.
(1)求 ;
;
(2)设直线MF与抛物线交于C,D两点,且四边形ACBD的面积为 ,求直线AB的斜率k.
,求直线AB的斜率k. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
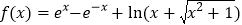 (其中
(其中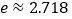 ),若对任意的
),若对任意的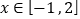 ,
, 恒成立,则实数
恒成立,则实数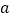 的取值范围是________________.
的取值范围是________________. -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校有120名教师,且年龄都在20岁到60岁之间,各年龄段人数按分组,其频率分布直方图如图所示,学校要求每名教师都要参加两项培训,培训结束后进行结业考试.已知各年龄段两项培训结业考试成绩优秀的人数如表示,假设两项培训是相互独立的,结业考试成绩也互不影响.
年龄分组
A项培训成绩优秀人数
B项培训成绩优秀人数
[20,30)
30
18
[30,40)
36
24
[40,50)
12
9
[50,60]
4
3
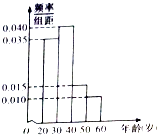
(1)若用分层抽样法从全校教师中抽取一个容量为40的样本,求从年龄段[20,30)抽取的人数;
(2)求全校教师的平均年龄;
(3)随机从年龄段[20,30)和[30,40)内各抽取1人,设这两人中两项培训结业考试成绩都优秀的人数为X,求X的概率分布和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和为Sn , 常数λ>0,且λa1an=S1+Sn对一切正整数n都成立.
(1)求数列{an}的通项公式;
(2)设a1>0,λ=100,当n为何值时,数列 的前n项和最大?
的前n项和最大? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
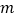 ,
,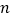 是两条不同直线,
是两条不同直线,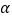 ,
,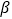 是两个不同平面,则下列命题正确的是 ( )
是两个不同平面,则下列命题正确的是 ( )A. 若
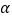 ,
,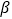 垂直于同一平面,则
垂直于同一平面,则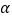 与
与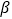 平行
平行B. 若
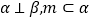 ,则
,则
C. 若
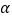 ,
,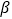 不平行,则在
不平行,则在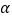 内不存在与
内不存在与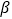 平行的直线
平行的直线D. 若
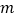 ,
,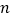 不平行,则
不平行,则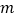 与
与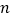 不可能垂直于同一平面
不可能垂直于同一平面 -
科目: 来源: 题型:
查看答案和解析>>【题目】根据市场分析,某蔬菜加工点,当月产量为10吨至25吨时,月生产总成本
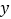 (万元)可以看出月产量
(万元)可以看出月产量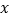 (吨)的二次函数,当月产量为10吨时,月生产成本为20万元,当月产量为15吨时,月生产总成本最低至17.5万元.
(吨)的二次函数,当月产量为10吨时,月生产成本为20万元,当月产量为15吨时,月生产总成本最低至17.5万元.(I)写出月生产总成本
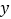 (万元)关于月产量
(万元)关于月产量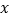 吨的函数关系;
吨的函数关系;(II)已知该产品销售价为每吨1.6万元,那么月产量为多少吨时,可获得最大利润,并求出最大利润.
相关试题

