【题目】已知函数![]() (
(![]() ),将
),将![]() 的图象向左平移
的图象向左平移![]() 个单位长度后得到
个单位长度后得到![]() 的图象,且
的图象,且![]() 在区间
在区间![]() 内的最大值为
内的最大值为![]() .
.
(1)求实数![]() 的值;
的值;
(2)在![]() 中,内角
中,内角![]() ,
, ![]() ,
, ![]() 的对边分别是
的对边分别是![]() ,
, ![]() ,
, ![]() ,若
,若![]() ,且
,且![]() ,求
,求![]() 的周长
的周长![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() .(2)
.(2)![]()
【解析】试题分析:(1)先利用两角和公式和对函数解析式化简整理,根据图象的平移确定![]() 的解析式,根据
的解析式,根据![]() 的范围和三角函数的图象与性质确定
的范围和三角函数的图象与性质确定![]() 的最大值的解析式,求得
的最大值的解析式,求得![]() ;(2)根据第一问中函数的解析式确定
;(2)根据第一问中函数的解析式确定![]() 的值,进而利用余弦定理和基本不等式确定
的值,进而利用余弦定理和基本不等式确定![]() 的范围,最后确定周长的范围.
的范围,最后确定周长的范围.
试题解析:(1)由题设得![]()
![]() .
.
所以![]()
![]() .
.
因为当![]() 时,
时, ![]() .
.
令![]() ,即
,即![]() 时,
时, ![]() ,所以
,所以![]() .
.
(2)由已知得![]() .因为在
.因为在![]() 中,
中, ![]() ,所以
,所以![]() ,
,
所以![]() ,所以
,所以![]() ,即
,即![]() .
.
又因为![]() ,由余弦定理,得
,由余弦定理,得
![]()
![]()
![]()
![]() ,当且仅当
,当且仅当![]() 时等号成立.又因为
时等号成立.又因为![]() ,所以
,所以![]() ,所以
,所以![]() 的周长
的周长![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知曲线
 的参数方程为
的参数方程为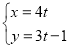 (
(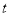 为参数),当
为参数),当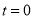 时,曲线
时,曲线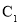 上对应的点为
上对应的点为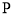 .以原点
.以原点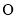 为极点,以
为极点,以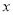 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线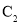 的极坐标方程为
的极坐标方程为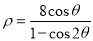 .
.(I)求曲线
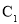 的普通方程和曲线
的普通方程和曲线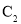 的直角坐标方程;
的直角坐标方程;(II)设曲线
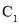 与
与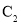 的公共点为
的公共点为 ,
,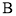 ,求
,求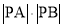 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】椭圆
 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在 轴上,焦点到短轴端点的距离为2,离心率为
轴上,焦点到短轴端点的距离为2,离心率为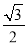 .
.(Ⅰ)求该椭圆的方程;
(Ⅱ)若直线
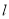 与椭圆
与椭圆 交于
交于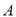 ,
, 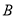 两点且
两点且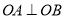 ,是否存在以原点
,是否存在以原点 为圆心的定圆与直线
为圆心的定圆与直线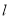 相切?若存在求出定圆的方程;若不存在,请说明理由
相切?若存在求出定圆的方程;若不存在,请说明理由 -
科目: 来源: 题型:
查看答案和解析>>【题目】
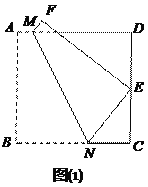
问题解决
如图(1),将正方形纸片ABCD折叠,使点B落在CD边上一点E(不与点C、D重合),压平后得到折痕MN.当
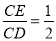 时,求
时,求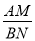 的值.
的值.类比归纳
在图(1)中,若
 则
则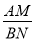 的值等于 ;若
的值等于 ;若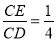 则
则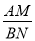 的值等于 ;若
的值等于 ;若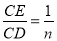 (n为整数),则
(n为整数),则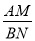 的值等于 .(用含
的值等于 .(用含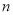 的式子表示)
的式子表示)联系拓广
如图(2),将矩形纸片ABCD折叠,使点B落在CD边上一点E(不与点C、D重合),压平后得到折痕MN设
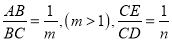 ,则
,则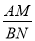 的值等
的值等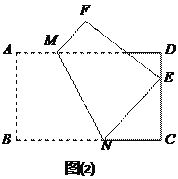
 于 ▲ .(用含
于 ▲ .(用含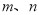 的式子表示)
的式子表示) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形
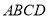 中,
中,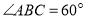 ,
,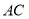 与
与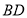 相交于点
相交于点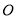 ,
,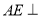 平面
平面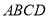 ,
,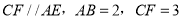 .
.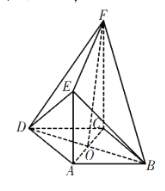
(1)求证:
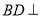 平面
平面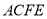 ;
;(2)当直线
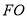 与平面
与平面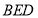 所成角的大小为
所成角的大小为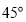 时,求
时,求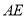 的长度.
的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】某水泥厂销售工作人员根据以往该厂的销售情况,绘制了该厂日销售量的频率分布直方图,如图所示:
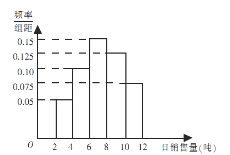
将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.
(1)求未来3天内,连续2天日销售量不低于8吨,另一天日销售量低于8吨的概率;
(2)用
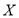 表示未来3天内日销售量不低于8吨的天数,求随机变量
表示未来3天内日销售量不低于8吨的天数,求随机变量 的分布列及数学期望.
的分布列及数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列
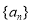 满足:
满足: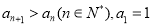 ,该数列的前三项分别加上1,1,3后成等比数列,且
,该数列的前三项分别加上1,1,3后成等比数列,且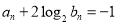 .
.(1)求数列
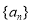 ,
,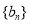 的通项公式;
的通项公式;(2)求数列
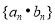 的前
的前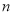 项和
项和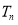 .
.
相关试题

