Question

【题目】已知函数f（x）=|xex|，方程f2（x）+tf（x）+1=0（t∈R）有四个实数根，则t的取值范围

Answer 1

【答案】
【解析】f（x）=|xex|=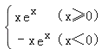
当x≥0时，f′（x）=ex+xex≥0恒成立，所以f（x）在[0，+∞）上为增函数；
当x＜0时，f′（x）=﹣ex﹣xex=﹣ex（x+1），
由f′（x）=0，得x=﹣1，当x∈（﹣∞，﹣1）时，f′（x）=﹣ex（x+1）＞0，f（x）为增函数，
当x∈（﹣1，0）时，f′（x）=﹣ex（x+1）＜0，f（x）为减函数，
所以函数f（x）=|xex|在（﹣∞，0）上有一个极大值为f（﹣1）=﹣（﹣1）e﹣1= ，
要使方程f2（x）+tf（x）+1=0（t∈R）有四个实数根，
令f（x）=m，则方程m2+tm+1=0应有两个不等根，且一个根在(0,)内，一个根在(,+)内，
再令g（m）=m2+tm+1，
因为g（0）=1＞0，
则只需g（）＜0，即 ， 解得：t＜﹣ ．
所以，使得函数f（x）=|xex|，方程f2（x）+tf（x）+1=0（t∈R）有四个实数根的t的取值范围
是 ．
故答案为 ．
函数f（x）=|xex|是分段函数，通过求导分析得到函数f（x）在（0，+∞）上为增函数，在（﹣∞，﹣1）上为增函数，在（﹣1，0）上为减函数，求得函数f（x）在（﹣∞，0）上，当x=﹣1时有一个最大值 ， 所以，要使方程f2（x）+tf（x）+1=0（t∈R）有四个实数根，f（x）的值一个要在(0,)内，一个在(,+)内，然后运用二次函数的图象及二次方程根的关系列式求解t的取值范围．