【题目】在![]() 中,
中,![]() 分别为角
分别为角![]() 的对边,设
的对边,设![]() .
.
(1)若![]() ,且
,且![]() ,求角
,求角![]() 的大小;
的大小;
(2)若![]() ,求角
,求角![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)由题意可得:a2-(a2-b2)-4c2=0,即可得到b=2c,根据正弦定理可得:sinB=2sinC,又![]() ,再结合角C的范围求出答案即可.
,再结合角C的范围求出答案即可.
(2)由题意可得:a2+b2=2c2,根据余弦定理可得:![]() ,再由2c2=a2+b2≥2ab可得ab≤c2,进而求出cosC的范围即可根据余弦函数求出角C的范围.
,再由2c2=a2+b2≥2ab可得ab≤c2,进而求出cosC的范围即可根据余弦函数求出角C的范围.
试题解析:
(1)由![]() ,得
,得![]() ,∴
,∴![]() ,
,
又由正弦定理,得![]() ,
,![]() ,将其代入上式,得
,将其代入上式,得![]() ,
,
∵![]() ,∴
,∴![]() ,将其代入上式,得
,将其代入上式,得![]() ,
,
∴![]() ,整理得:
,整理得:![]() ,∴
,∴![]() .
.
∵角![]() 是三角形的内角,∴
是三角形的内角,∴![]() .
.
(2)∵![]() ,∴
,∴![]() ,即
,即![]() ,
,
由余弦定理,得![]() ,
,
∴![]() (当且仅当
(当且仅当![]() 时取等号).
时取等号).
∴![]() ,
,![]() 是锐角,又∵余弦函数在
是锐角,又∵余弦函数在![]() 上递减,∴
上递减,∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4.
(1)从袋中随机取出两个球,求取出的球的编号之和不大于4的概率.
(2)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,该球的编号为n,求n<m+2的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于120分为优秀,120分以下为非优秀.统计成绩后,得到如下的
 列联表,且已知在甲、乙两个文科班全部110人中随机抽1人为优秀的概率为
列联表,且已知在甲、乙两个文科班全部110人中随机抽1人为优秀的概率为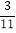 .
.优秀
非优秀
合计
甲班
10
乙班
30
合计
110
Ⅰ.请完成上面的列联表;
Ⅱ.根据列联表的数据,是否有
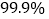 的把握认为“成绩与班级有关系”.
的把握认为“成绩与班级有关系”.参考公式与临界值表:
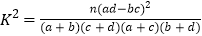 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
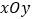 中,曲线
中,曲线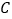 :
: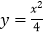 与直线
与直线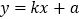 (
( )交于
)交于 ,
,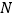 两点.
两点.(1)当
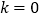 时,分别求
时,分别求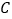 在点
在点 和
和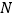 处的切线方程;
处的切线方程;(2)
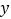 轴上是否存在点
轴上是否存在点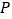 ,使得当
,使得当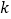 变动时,总有
变动时,总有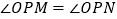 ?说明理由.
?说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
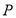 是椭圆
是椭圆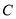 上任一点,点
上任一点,点 到直线
到直线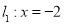 的距离为
的距离为 ,到点
,到点 的距离为
的距离为 ,且
,且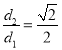 .直线
.直线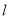 与椭圆
与椭圆 交于不同两点
交于不同两点 (
( 都在
都在 轴上方),且
轴上方),且 .
.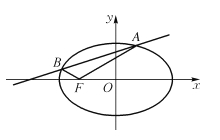
(1)求椭圆
 的方程;
的方程;(2)当
 为椭圆与
为椭圆与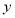 轴正半轴的交点时,求直线
轴正半轴的交点时,求直线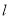 方程;
方程;(3)对于动直线
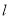 ,是否存在一个定点,无论
,是否存在一个定点,无论 如何变化,直线
如何变化,直线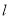 总经过此定点?若存在,求出该定点的坐标;若不存在,请说明理由.
总经过此定点?若存在,求出该定点的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】长时间用手机上网严重影响着学生的身体健康,某校为了解
 两班学生手机上网的时长,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周手机上网的时长作为样本,绘制成茎叶图如图所示(图中茎叶表示十位数字,叶表示个位数字).
两班学生手机上网的时长,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周手机上网的时长作为样本,绘制成茎叶图如图所示(图中茎叶表示十位数字,叶表示个位数字).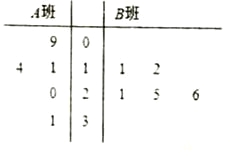
(1)分别求出图中所给两组样本数据的平均值,并据此估计,哪个班的学生平均上网时间较长;
(2)从
 班的样本数据中随机抽取一个不超过19的数据记为
班的样本数据中随机抽取一个不超过19的数据记为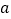 ,从
,从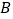 班的样本数据中随机抽取一个不超过21的数据记为
班的样本数据中随机抽取一个不超过21的数据记为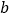 ,求
,求 的概率.
的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列4个命题:
①为了了解800名学生对学校某项教改试验的意见,打算从中抽取一个容量为40的样本,考虑用系统抽样,则分段的间隔为40;
②四边形
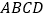 为长方形,
为长方形,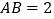 ,
,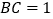 ,
,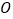 为
为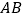 中点,在长方形
中点,在长方形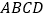 内随机取一点
内随机取一点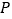 ,取得的
,取得的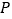 点到
点到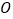 的距离大于1的概率为
的距离大于1的概率为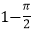 ;
;③把函数
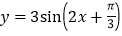 的图象向右平移
的图象向右平移 个单位,可得到
个单位,可得到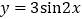 的图象;
的图象;④已知回归直线的斜率的估计值为
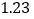 ,样本点的中心为
,样本点的中心为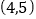 ,则回归直线方程为
,则回归直线方程为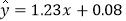 .
.其中正确的命题有__________.(填上所有正确命题的编号)
相关试题

