【题目】判断下列命题是全称命题还是特称命题,并判断其真假.
(1)对数函数都是单调函数;
(2)至少有一个整数,它既能被11整除,又能被9整除;
(3)x∈{x|x>0}, ![]() ;
;
(4)x0∈Z,log2x0>2.
参考答案:
【答案】见解析
【解析】试题分析:根据全称命题和特称命题的定义,全称命题要包含全称量词,特称命题要包含特称量词,我们逐一分析四个命题(1)中隐含“所有”,(2)中含至少,(3)中含任意,(4)中含存在,易得到答案.
试题解析:(1)本题隐含了全称量词“所有的”,可表述为“所有的对数函数都是单调函数”,是全称命题,且为真命题.
(2)命题中含有存在量词“至少有一个”,因此是特称命题,真命题.
(3)命题中含有全称量词“”,是全称命题,真命题;
(4)命题中含有存在量词“”,是特称命题,真命题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若要按从大到小给7,5,9,3,10五个数排序,试写出算法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出如图所示的对应:
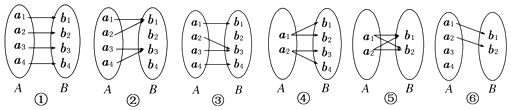
其中构成从A到B的映射的个数为( )
A.3
B.4
C.5
D.6 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a>0,a≠1.设命题p:函数y=loga(x+1)在(0,+∞)内单调递减;命题q:曲线y=x2+(2a-3)x+1与x轴交于不同的两点.若p或q为真,p且q为假,求a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知命题:“x∈{x|-1≤x≤1},都有不等式x2-x-m<0成立”是真命题.
(1)求实数m的取值集合B;
(2)设不等式(x-3a)(x-a-2)<0的解集为A,若x∈A是x∈B的充分不必要条件,求实数a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设M={x|0≤x≤2},N={y|0≤y≤2},给出下列四个图形:
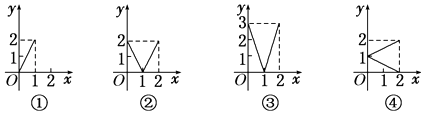
其中,能表示从集合M到集合N的函数关系的个数是( )
A.0
B.1
C.2
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2﹣6x+8,x∈[1,a],并且函数f(x)的最小值为f(a),则实数a的取值范围是 .
相关试题

