【题目】已知数列{an}是等差数列,Sn为{an}的前n项和,且a10=19,S10=100;数列{bn}对任意n∈N* , 总有b1b2b3…bn﹣1bn=an+2成立.
(1)求数列{an}和{bn}的通项公式;
(2)记cn=(﹣1)n ![]() ,求数列{cn}的前n项和Tn .
,求数列{cn}的前n项和Tn .
参考答案:
【答案】
(1)
解:设{an}的公差为d,
则a10=a1+9d=19, ![]() ,
,
解得a1=1,d=2,所以an=2n﹣1,
所以b1b2b3…bn﹣1bn=2n+1…①
当n=1时,b1=3,
当n≥2时,b1b2b3…bn﹣1=2n﹣1…②
①②两式相除得 ![]()
因为当n=1时,b1=3适合上式,所以 ![]() .
.
(2)
解:由已知 ![]() ,
,
得 ![]()
则Tn=c1+c2+c3+…+cn= ![]() ,
,
当n为偶数时, ![]()
= ![]()
= ![]() ,
,
当n为奇数时, ![]()
= ![]()
= ![]() .
.
综上:  .
.
【解析】(1)由题意和等差数列的前n项和公式求出公差,代入等差数列的通项公式化简求出an , 再化简b1b2b3…bn﹣1bn=an+2,可得当n≥2时b1b2b3…bn﹣1=2n﹣1,将两个式子相除求出bn;(2)由(1)化简cn=(﹣1)n ![]() ,再对n分奇数和偶数讨论,分别利用裂项相消法求出Tn , 最后要用分段函数的形式表示出来.
,再对n分奇数和偶数讨论,分别利用裂项相消法求出Tn , 最后要用分段函数的形式表示出来.
【考点精析】本题主要考查了等差数列的前n项和公式和数列的前n项和的相关知识点,需要掌握前n项和公式:![]() ;数列{an}的前n项和sn与通项an的关系
;数列{an}的前n项和sn与通项an的关系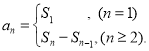 才能正确解答此题.
才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 关于直线
关于直线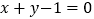 对称,圆心
对称,圆心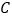 在第二象限,半径为
在第二象限,半径为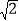 .
.(Ⅰ)求圆
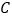 的方程.
的方程.(Ⅱ)是否存在直线
 与圆
与圆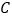 相切,且在
相切,且在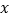 轴、
轴、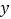 轴上的截距相等?若存在,写出满足条件的直线条数(不要求过程);若不存在,说明理由.
轴上的截距相等?若存在,写出满足条件的直线条数(不要求过程);若不存在,说明理由. -
科目: 来源: 题型:
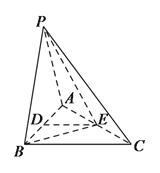
查看答案和解析>>【题目】如图,在三棱锥
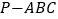 中,
中,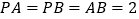 ,
,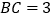 ,
,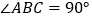 ,平面
,平面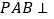 平面
平面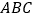 ,
,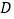 、
、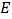 分别为
分别为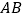 、
、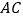 中点.
中点.(Ⅰ)求证:
 平面
平面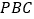 .
.(Ⅱ)求证:
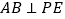 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
已知圆
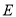 的极坐标方程为
的极坐标方程为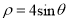 ,以极点为原点,极轴为
,以极点为原点,极轴为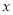 轴的正半轴建立平面直角坐标系,取相同单位长度(其中
轴的正半轴建立平面直角坐标系,取相同单位长度(其中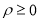 ,
, 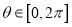 ),若倾斜角为
),若倾斜角为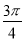 且经过坐标原点的直线
且经过坐标原点的直线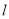 与圆
与圆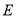 相交于点
相交于点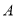 (
(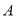 点不是原点).
点不是原点).(1)求点
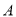 的极坐标;
的极坐标;(2)设直线
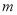 过线段
过线段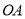 的中点
的中点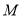 ,且直线
,且直线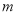 交圆
交圆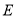 于
于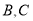 两点,求
两点,求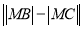 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的各项均为正数,其前n项和为Sn , 且满足a1=1,an+1=2
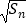 +1,n∈N* .
+1,n∈N* .
(1)求a2的值;
(2)求数列{an}的通项公式;
(3)是否存在正整数k,使ak , S2k﹣1 , a4k成等比数列?若存在,求k的值,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义在
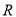 上的函数
上的函数 ,如果存在函数
,如果存在函数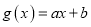 (
(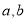 为常数),使得
为常数),使得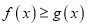 对一切实数
对一切实数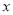 都成立,则称
都成立,则称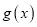 为函数
为函数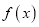 的一个承托函数,给出如下命题:
的一个承托函数,给出如下命题:①函数
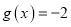 是函数
是函数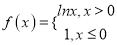 的一个承托函数;
的一个承托函数;②函数
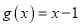 是函数
是函数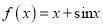 的一个承托函数;
的一个承托函数;③若函数
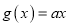 是函数
是函数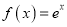 的一个承托函数,则
的一个承托函数,则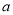 的取值范围是
的取值范围是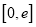 ;
;④值域是
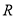 的函数
的函数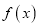 不存在承托函数.
不存在承托函数.其中正确的命题的个数为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某正三棱柱的三视图如图所示,其中正(主)视图是边长为
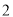 的正方形,该正三棱柱的表面积是( ).
的正方形,该正三棱柱的表面积是( ).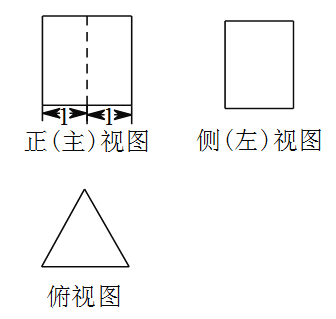
A.
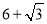 B.
B. 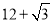 C.
C. 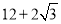 D.
D. 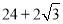
相关试题

