搜索
【题目】已知曲线C的极坐标方程是ρ＝2,以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为
(t为参数).
(1)写出直线l的普通方程与曲线C的直角坐标方程;
(2)设曲线C经过伸缩变换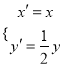
得到曲线,设M(x,y)为
上任意一点,求
的最小值,并求相应的点M的坐标.
参考答案：
【答案】（1）
， 
；（2）当M为
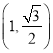或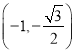
时原式取得最小值1.
【解析】试题分析：(1)将直线中的参数消去，即可得到其普通方程，在极坐标方程
两边平方，由
替换即可得到圆的直角坐标方程．(2)由变换公式先写出变换后的方程为一椭圆，用椭圆的参数方程表示点
代入
，由三角函数知识求之即可．
试题解析：（1）由
，得
，代入
，
得直线的普通方程
．
由
，得
，∴
．
（2）∵
，∴
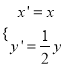的直角坐标方程为
．
∴设
，则
．
∴
．
∴当
，即
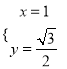或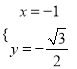
，上式取最小值
．
即当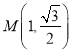
或
， 
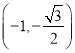的最小值为
．
-
科目： 来源： 题型：
查看答案和解析>>【题目】家政服务公司根据用户满意程度将本公司家政服务员分为两类，其中A类服务员12名，B类服务员x名．
(Ⅰ)若采用分层抽样的方法随机抽取20名家政服务员参加技术培训，抽取到B类服务员的人数是16, 求x的值；
(Ⅱ)某客户来公司聘请2名家政服务员，但是由于公司人员安排已经接近饱和，只有3名A类家政服务员和2名B类家政服务员可供选择，求该客户最终聘请的家政服务员中既有A类又有B类的概率．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知椭圆C：
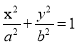(a>b>0)，长轴长为4，离心率为
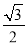.(Ⅰ)椭圆的求椭圆的标准方程；
(Ⅱ)设过定点M(0,2)的直线l与椭圆C交于不同的两点A，B，且∠AOB为锐角(O为坐标原点)，求直线l的斜率k的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f(x)＝x2－ax＋2lnx，a∈R.
(Ⅰ)若曲线y＝f(x)在(1，f(1))处的切线垂直于直线y＝x，求函数f(x)的单调区间；
(Ⅱ)若x>1时，f(x)>0恒成立，求实数a的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f(x)＝|x－1|.
(Ⅰ)解不等式f(x)＋f(x＋4)≥8；
(Ⅱ)若|a|<1，|b|<1，且a≠0，求证：f(ab)>|a|f(
)． -
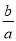科目： 来源： 题型：
查看答案和解析>>【题目】已知函数
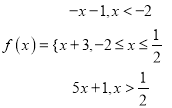
(1)求函数f(x)的最小值；
(2)已知m∈R，p：关于x的不等式f(x)≥m2＋2m－2对任意x∈R恒成立，q：函数y＝(m2－1)x是增函数，若p正确，q错误，求实数m的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】设向量
， 
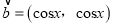，记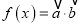
(1)求函数f(x)的最小正周期；
(2)试用“五点法”画出函数f(x)在区间
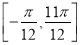上的简图，并指出该函数的图象可由y＝sin x(x∈R)的图象经过怎样的平移和伸缩变换得到；(3)若函数g(x)＝f(x)＋m，
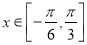的最小值为2，试求出函数g(x)的最大值．
相关试题
