【题目】已知函数![]()
(1)若函数![]() 在定义域内单调递增,求实数
在定义域内单调递增,求实数 ![]() 的取值范围,
的取值范围,
(2)当![]() 时,关于
时,关于![]() 的方程
的方程![]() 在[1,4]上恰有两个不相等的实数根,
在[1,4]上恰有两个不相等的实数根,
求实数的取值范围。
参考答案:
【答案】(1) (﹣∞,﹣1];(2) ln2﹣2<b≤﹣![]()
【解析】试题分析:(1)对函数f(x)进行求导,令导数大于等于0在x>0上恒成立即可.
(2)将a的值代入整理成方程的形式,然后转化为函数考虑其图象与x轴的交点的问题.
试题解析:
(1)f′(x)=﹣![]() ,(x>0)
,(x>0)
依题意f'(x)≥0在x>0时恒成立,即ax2+2x﹣1≤0在x>0恒成立.
则a≤![]() =(
=( ![]() ﹣1)2﹣1在x>0恒成立,
﹣1)2﹣1在x>0恒成立,
即a≤((![]() ﹣1)2﹣1)min(x>0)
﹣1)2﹣1)min(x>0)
当x=1时,(![]() ﹣1)2﹣1取最小值﹣1,
﹣1)2﹣1取最小值﹣1,
∴a的取值范围是(﹣∞,﹣1].
(2)a=﹣![]() ,f(x)=﹣
,f(x)=﹣![]() x+b,
x+b,
∴![]() x2﹣
x2﹣![]() x+lnx﹣b=0
x+lnx﹣b=0
设g(x)=![]() x2﹣
x2﹣![]() x+lnx﹣b(x>0)则g'(x)=
x+lnx﹣b(x>0)则g'(x)=![]() ,
,
列表:
X | (0,1) | 1 | (1,2) | 2 | (2,4) |
g′(x) | + | 0 | ﹣ | 0 | + |
g(x) | ↑ | 极大值 | ↓ | 极小值 | ↑ |
∴g(x)极小值=g(2)=ln2﹣b﹣2,g(x)极大值=g(1)=﹣b﹣![]() ,
,
又g(4)=2ln2﹣b﹣2
∵方程g(x)=0在[1,4]上恰有两个不相等的实数根.
则  ,得:ln2﹣2<b≤﹣
,得:ln2﹣2<b≤﹣![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,动点满足
,动点满足 成等差数列。
成等差数列。(1)求点
 的轨迹方程;
的轨迹方程;(2)对于
 轴上的点
轴上的点 ,若满足
,若满足 ,则称点
,则称点 为点
为点 对应的“比例点”,问:对任意一个确定的点
对应的“比例点”,问:对任意一个确定的点 ,它总能对应几个“比例点”?
,它总能对应几个“比例点”? -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,
 为坐标原点,已知两点
为坐标原点,已知两点 、
、 在
在 轴的正半轴上,点
轴的正半轴上,点 在
在 轴的正半轴上.若
轴的正半轴上.若 ,
, .
.(
 )求向量
)求向量 ,
, 夹角的正切值.
夹角的正切值.(
 )问点
)问点 在什么位置时,向量
在什么位置时,向量 ,
, 夹角最大?
夹角最大? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 ,直线
,直线 与E交于A、B两点,且
与E交于A、B两点,且 ,其中O为原点.
,其中O为原点.(1)求抛物线E的方程;
(2)点C坐标为
 ,记直线CA、CB的斜率分别为
,记直线CA、CB的斜率分别为 ,证明:
,证明:  为定值.
为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知
 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 ,其中
,其中 且
且 .设
.设 .
.(
 )若
)若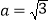 ,
, ,
, ,求方程
,求方程 在区间
在区间 内的解集.
内的解集.(
 )若函数
)若函数 满足:图象关于点
满足:图象关于点 对称,在
对称,在 处取得最小值,试确定
处取得最小值,试确定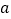 、
、 和
和 应满足的与之等价的条件.
应满足的与之等价的条件. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 的焦点为
的焦点为 ,点
,点 在抛物线
在抛物线 上,且
上,且 。
。(Ⅰ)求抛物线
 的标准方程及实数
的标准方程及实数 的值;
的值;(Ⅱ)直线
 过抛物线
过抛物线 的焦点
的焦点 ,且与抛物线
,且与抛物线 交于
交于 两点,若
两点,若 (
( 为坐标原点)的面积为
为坐标原点)的面积为 ,求直线
,求直线 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
 的前
的前 项和为
项和为 ,其中
,其中 为常数.
为常数.(1)证明:
 ;
;(2)是否存在
 ,使得
,使得 为等差数列?并说明理由.
为等差数列?并说明理由.
相关试题

