【题目】设![]() 实数
实数![]() 满足不等式
满足不等式![]() 函数
函数![]() 无极值点.
无极值点.
(1)若“![]() ”为假命题,“
”为假命题,“![]() ”为真命题,求实数
”为真命题,求实数![]() 的取值范围;
的取值范围;
(2)已知“![]() ”为真命题,并记为
”为真命题,并记为![]() ,且
,且![]() ,若
,若![]() 是
是![]() 的必要不充分条件,求正整数
的必要不充分条件,求正整数![]() 的值.
的值.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:由![]() ,得
,得![]() ;函数
;函数![]() 无极值点,
无极值点,![]() 恒成立,得
恒成立,得![]() ,解得
,解得![]() .(1)“
.(1)“![]() ”为假命题,“
”为假命题,“![]() ”为真命题,则
”为真命题,则![]() 与
与![]() 只有一个命题是真命题,分成
只有一个命题是真命题,分成![]() 真
真![]() 假和
假和![]() 假
假![]() 真两类来求
真两类来求![]() 的取值范围;(2)“
的取值范围;(2)“![]() ”为真命题,两个都是真命题,所以
”为真命题,两个都是真命题,所以![]() .将
.将![]() 因式分解得
因式分解得![]() ,解得
,解得![]() 或
或![]() ,
,![]() ,
,![]() 是
是![]() 的必要不充分条件得
的必要不充分条件得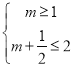 ,解得
,解得![]() ,所以
,所以![]() .
.
试题解析:
由![]() ,得
,得![]() ,即
,即![]() ................1分
................1分
∵函数![]() 无极值点,∴
无极值点,∴![]() 恒成立,得
恒成立,得![]() ,解得
,解得![]() ,
,
即![]() ..................................3分
..................................3分
(1)∵“![]() ”为假命题,“
”为假命题,“![]() ”为真命题,∴
”为真命题,∴![]() 与
与![]() 只有一个命题是真命题.
只有一个命题是真命题.
若![]() 为真命题,
为真命题,![]() 为假命题,则
为假命题,则![]() ;.....................5分
;.....................5分
若![]() 为真命题,
为真命题,![]() 为假命题,则
为假命题,则![]() ..............6分
..............6分
于是,实数![]() 的取值范围为
的取值范围为![]() .....................7分
.....................7分
(2)∵“![]() ”为真命题,∴
”为真命题,∴![]() ..............8分
..............8分
又![]() ,
,
∴![]() ,
,
∴![]() 或
或![]() ,...................10分
,...................10分
即![]() 或
或![]() ,从而
,从而![]() ,
,
∵![]() 是
是![]() 的必要不充分条件,即
的必要不充分条件,即![]() 是
是![]() 的充分不必要条件,
的充分不必要条件,
∴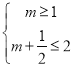 ,解得
,解得![]() ,∵
,∵![]() ,∴
,∴![]() ..................12分
..................12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
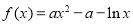 ,
,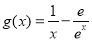 ,其中
,其中 ,
,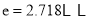 为自然对数的底数.
为自然对数的底数.(1)讨论
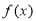 的单调性;
的单调性;(2)证明:当
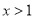 时,
时,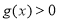 ;
;(3)确定
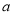 的所有可能取值,使得
的所有可能取值,使得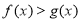 在
在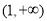 区间内恒成立.
区间内恒成立. -
科目: 来源: 题型:
查看答案和解析>>【题目】设y1=
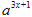 ,y2=
,y2=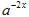 ,其中a>0,且a≠1,试确定x为何值时,有:
,其中a>0,且a≠1,试确定x为何值时,有:(1)y1=y2;(2)y1>y2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了迎接世博会,某旅游区提倡低碳生活,在景区提供自行车出租.该景区有50辆自行车供游客租赁使用,管理这些自行车的费用是每日115元.根据经验,若每辆自行车的日租金不超过6元,则自行车可以全部租出;若超出6元,则每超过1元,租不出的自行车就增加3辆.为了便于结算,每辆自行车的日租金
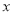 (元)只取整数,并且要求出租自行车一日的总收入必须高于这一日的管理费用,用
(元)只取整数,并且要求出租自行车一日的总收入必须高于这一日的管理费用,用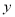 (元)表示出租自行车的日净收入(即一日中出租自行车的总收入减去管理费用后的所得)。
(元)表示出租自行车的日净收入(即一日中出租自行车的总收入减去管理费用后的所得)。(1)求函数
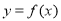 的解析式及其定义域;
的解析式及其定义域;(2)试问当每辆自行车的日租金定为多少元时,才能使一日的净收入最多?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知某运动员每次投篮命中的概率都为40%,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中;5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果,经随机模拟产生了如下20组随机数:
137 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,该运动员三次投篮恰有两次命中的概率为( )
A.0.40 B.0.30
C.0.35 D.0.25
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
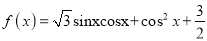 .
.(1)当
 时,求函数
时,求函数 的值域;
的值域;(2)已知
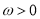 ,函数
,函数 ,若函数
,若函数 在区间
在区间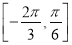 上是增函数,求
上是增函数,求 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
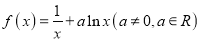 .
.(1)若
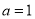 ,求
,求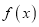 的极值和单调区间;
的极值和单调区间;(2)若在区间
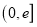 上至少存在一点
上至少存在一点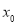 ,使得
,使得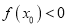 成立,求实数
成立,求实数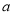 的取值范围.
的取值范围.
相关试题

