【题目】如图,在△ABC中,D为边BC上一点,AD=6,BD=3,DC=2.
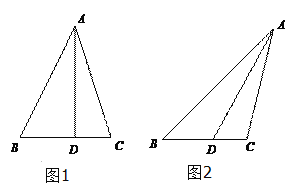
(1)若AD⊥BC,求∠BAC的大小;
(2)若∠ABC=![]() ,求△ADC的面积.
,求△ADC的面积.
参考答案:
【答案】(1)∠BAC=![]() .(2)
.(2)![]() (1+
(1+![]() )
)
【解析】 试题分析:(1)设![]() ,可得
,可得![]() ,即可求解
,即可求解![]() 的值,得到结论;
的值,得到结论;
(2)设![]() ,得
,得![]() ,在
,在![]() 中,由正弦定理,得出
中,由正弦定理,得出![]() ,进而得到
,进而得到![]() 的值,利用两角和的正弦函数,即可求解结论。
的值,利用两角和的正弦函数,即可求解结论。
试题解析:
(1)设∠BAD=α,∠DAC=β.
因为AD⊥BC,AD=6,BD=3,DC=2,
所以tanα=,tanβ=,所以tan∠BAC=tan(α+β)=![]() =
=![]() =1.
=1.
又∠BAC∈(0,π),所以∠BAC=![]() .
.
(2)设∠BAD=α.
在△ABD中,∠ABC=![]() ,AD=6,BD=3.
,AD=6,BD=3.
由正弦定理得![]() =
=![]() , 解得sinα=
, 解得sinα=![]() .
.
因为AD>BD,所以α为锐角,从而cosα=![]() =
=![]() .
.
因此sin∠ADC=sin(α+![]() )=sinαcos
)=sinαcos![]() +cosαsin
+cosαsin![]()
=![]() (
(![]() +
+![]() )=
)=![]() .
.
△ADC的面积S=×AD×DC·sin∠ADC
=×6×2×![]() = (1+
= (1+![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两位小学生各有2008年奥运吉祥物“福娃”5个(其中“贝贝”、“晶晶”、“欢欢”、“迎迎”和“妮妮各一个”),现以投掷一个骰子的方式进行游戏,规则如下:当出现向上的点数是奇数时,甲赢得乙一个福娃;否则乙赢得甲一个福娃,规定掷骰子的次数达9次时,或在此前某人已赢得所有福娃时游戏终止.记游戏终止时投掷骰子的次数为ξ
(1)求掷骰子的次数为7的概率;
(2)求ξ的分布列及数学期望Eξ. -
科目: 来源: 题型:
查看答案和解析>>【题目】一家公司计划生产某种小型产品的月固定成本为1万元,每生产1万件需要再投入2万元,设该公司一个月内生产该小型产品x万件并全部销售完,每万件的销售收入为4﹣x万元,且每万件国家给予补助2e﹣
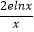 ﹣
﹣ 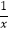 万元.(e为自然对数的底数,e是一个常数)
万元.(e为自然对数的底数,e是一个常数)
(1)写出月利润f(x)(万元)关于月产量x(万件)的函数解析式
(2)当月产量在[1,2e]万件时,求该公司在生产这种小型产品中所获得的月利润最大值(万元)及此时的月生成量值(万件).(注:月利润=月销售收入+月国家补助﹣月总成本) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
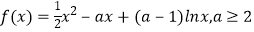 .
.
(1)求函数f(x)的单调区间;
(2)证明:若a<5,则对任意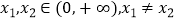 ,有
,有 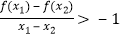 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于点E.

(1)若D为AC的中点,证明:DE是⊙O的切线;
(2)若OA= CE,求∠ACB的大小.
CE,求∠ACB的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
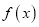 =ex(ex﹣a)﹣a2x.
=ex(ex﹣a)﹣a2x.(1)讨论
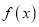 的单调性;
的单调性;(2)若
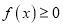 ,求a的取值范围.
,求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设A,B为曲线C:y=
 上两点,A与B的横坐标之和为4.
上两点,A与B的横坐标之和为4.(1)求直线AB的斜率;
(2)设M为曲线C上一点,C在M处的切线与直线AB平行,且AM
 BM,求直线AB的方程.
BM,求直线AB的方程.
相关试题

