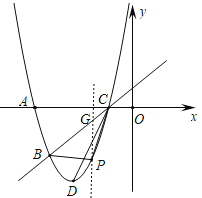
【题目】如图,已知抛物线![]() 经过
经过![]() ,
,![]() 两点,与
两点,与![]() 轴的另一个交点为
轴的另一个交点为![]() ,顶点为
,顶点为![]() ,连结
,连结![]() .
.

(1)求该抛物线的表达式;
(2)点![]() 为该抛物线上的一动点(与点
为该抛物线上的一动点(与点![]() 、
、![]() 不重合),设点
不重合),设点![]() 的横坐标为
的横坐标为![]() .当点
.当点![]() 在直线
在直线![]() 的下方运动时,求
的下方运动时,求![]() 的面积的最大值.
的面积的最大值.
参考答案:
【答案】(1)![]() (2)最大值为
(2)最大值为![]()
【解析】
(1)先由题意,得到![]() ,求出
,求出![]() ,即可得出结果;
,即可得出结果;
(2)先由抛物线的解析式,得到![]() ;过点
;过点![]() 作
作![]() 轴的平行线交
轴的平行线交![]() 于点
于点![]() ,求出直线
,求出直线![]() 的方程为:
的方程为:![]() ,设点
,设点![]() ,则点
,则点![]() ,表示出
,表示出![]() ,再由
,再由![]() ,根据二次函数的性质,即可得出结果.
,根据二次函数的性质,即可得出结果.
(1)因为抛物线![]() 经过
经过![]() ,
,![]() 两点,
两点,
所以![]() ,解得:
,解得:![]() ,
,
故抛物线的表达式为:![]() ;
;
(2)由![]() ,令
,令![]() ,则
,则![]() 或
或![]() (
(![]() 点舍去),即点
点舍去),即点![]() ;
;
如图,过点![]() 作
作![]() 轴的平行线交
轴的平行线交![]() 于点
于点![]() ,
,
又直线![]() 的斜率为
的斜率为![]() ,
,
所以直线![]() 的方程为:
的方程为:![]() ,
,
设点![]() ,则点
,则点![]() ,
,
所以![]() ,
,
因此![]()
![]() ,
,
∵![]() ,∴
,∴![]() 有最大值,当
有最大值,当![]() 时,其最大值为
时,其最大值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某群体的人均通勤时间,是指单日内该群体中成员从居住地到工作地的平均用时.某地上班族
 中的成员仅以自驾或公交方式通勤.分析显示:当
中的成员仅以自驾或公交方式通勤.分析显示:当 中
中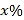 (
( )的成员自驾时,自驾群体的人均通勤时间为
)的成员自驾时,自驾群体的人均通勤时间为 (单位:分钟),而公交群体的人均通勤时间不受
(单位:分钟),而公交群体的人均通勤时间不受 影响,恒为
影响,恒为 分钟,试根据上述分析结果回答下列问题:
分钟,试根据上述分析结果回答下列问题:(1)当
 在什么范围内时,公交群体的人均通勤时间少于自驾群体的人均通勤时间?
在什么范围内时,公交群体的人均通勤时间少于自驾群体的人均通勤时间?(2)求该地上班族
 的人均通勤时间
的人均通勤时间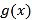 的表达式;讨论
的表达式;讨论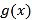 的单调性,并说明其实际意义.
的单调性,并说明其实际意义. -
科目: 来源: 题型:
查看答案和解析>>【题目】一只药用昆虫的产卵数y与一定范围内的温度x有关, 现收集了该种药用昆虫的6组观测数据如下表:
温度x/C
21
23
24
27
29
32
产卵数y/个
6
11
20
27
57
77
经计算得:
 ,
,  ,
,  ,
,  ,
,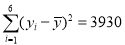 ,线性回归模型的残差平方和
,线性回归模型的残差平方和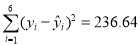 ,e8.0605≈3167,其中xi, yi分别为观测数据中的温度和产卵数,i=1, 2, 3, 4, 5, 6.
,e8.0605≈3167,其中xi, yi分别为观测数据中的温度和产卵数,i=1, 2, 3, 4, 5, 6.(Ⅰ)若用线性回归模型,求y关于x的回归方程
 =
= x+
x+ (精确到0.1);
(精确到0.1);(Ⅱ)若用非线性回归模型求得y关于x的回归方程为
 =0.06e0.2303x,且相关指数R2=0.9522.
=0.06e0.2303x,且相关指数R2=0.9522.( i )试与(Ⅰ)中的回归模型相比,用R2说明哪种模型的拟合效果更好.
( ii )用拟合效果好的模型预测温度为35C时该种药用昆虫的产卵数(结果取整数).
附:一组数据(x1,y1), (x2,y2), ...,(xn,yn ), 其回归直线
 =
= x+
x+ 的斜率和截距的最小二乘估计为
的斜率和截距的最小二乘估计为
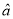 =
=
 ;相关指数R2=
;相关指数R2= .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为“中学数学联赛”选拔人才,分初赛和复赛两个阶段进行,规定:分数不小于本次考试成绩中位数的具有复赛资格,某校有900名学生参加了初赛,所有学生的成绩均在区间
 内,其频率分布直方图如图.
内,其频率分布直方图如图.
(1)求获得复赛资格应划定的最低分数线;
(2)从初赛得分在区间
 的参赛者中,利用分层抽样的方法随机抽取7人参加学校座谈交流,那么从得分在区间
的参赛者中,利用分层抽样的方法随机抽取7人参加学校座谈交流,那么从得分在区间 与
与 各抽取多少人?
各抽取多少人?(3)从(2)抽取的7人中,选出4人参加全市座谈交流,设
 表示得分在
表示得分在 中参加全市座谈交流的人数,学校打算给这4人一定的物质奖励,若该生分数在
中参加全市座谈交流的人数,学校打算给这4人一定的物质奖励,若该生分数在 给予500元奖励,若该生分数在
给予500元奖励,若该生分数在 给予800元奖励,用Y表示学校发的奖金数额,求Y的分布列和数学期望。
给予800元奖励,用Y表示学校发的奖金数额,求Y的分布列和数学期望。 -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
 中,圆
中,圆 的参数方程为
的参数方程为 (
( 为参数),圆
为参数),圆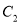 与圆
与圆 外切于原点
外切于原点 ,且两圆圆心的距离
,且两圆圆心的距离 ,以坐标原点为极点,
,以坐标原点为极点,  轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.(1)求圆
 和圆
和圆 的极坐标方程;
的极坐标方程;(2)过点
 的直线
的直线 与圆
与圆 异于点
异于点 的交点分别为点
的交点分别为点 ,与圆
,与圆 异于点
异于点 的交点分别为点
的交点分别为点 ,且
,且 ,求四边形
,求四边形 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知直线
 与双曲线
与双曲线 交于A,B两点,且点A的横坐标为4.
交于A,B两点,且点A的横坐标为4.(1)求
 的值及B点坐标;
的值及B点坐标;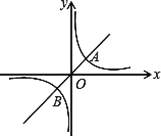
(2)结合图形,直接写出一次函数的函数值大于反比例函数的函数值时x的取值范围.
-
科目: 来源: 题型:
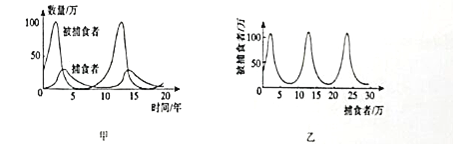
查看答案和解析>>【题目】图甲中的两条曲线分别表示某理想状态下捕食者和被捕食者数量随时间的变化规律、对捕食者和被捕食者数量之间的关系描述错误的是( )
A. 捕食者和被捕食者数量与时间以
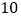 年为周期
年为周期B. 由图可知,当捕食者数量增多的过程中,被捕食者数量先增多后减少
C. 捕食者和被捕食者数量之间的关系可以用图1乙描述
D. 捕食者的数量在第
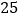 年和
年和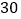 年之间数量在急速减少
年之间数量在急速减少
相关试题

