【题目】如图,在四棱锥![]() 中,
中, ![]() 为等边三角形,平面
为等边三角形,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点.
的中点.
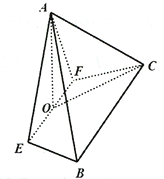
(1)求二面角![]() 的正弦值;
的正弦值;
(2)若![]() 平面
平面![]() ,求
,求![]() 的值.
的值.
参考答案:
【答案】(1)![]() (2)
(2)![]() .
.
【解析】试题分析:
(1)由题意可知![]() ,
, ![]() ,
, ![]() ,据此建立空间直角坐标系,计算可得平面
,据此建立空间直角坐标系,计算可得平面![]() 的法向量为
的法向量为![]() ,且平面
,且平面![]() 的一个法向量为
的一个法向量为![]() ,据此计算可得二面角的正弦值为
,据此计算可得二面角的正弦值为![]() .
.
(2)结合(1)中的空间直角坐标系有![]() ,据此得到关于实数a的方程:
,据此得到关于实数a的方程: ![]() ,解方程有:
,解方程有: ![]() .
.
试题解析:
(1)因为![]() 是等边三角形,
是等边三角形, ![]() 为
为![]() 的中点,所以
的中点,所以![]() ,
,
又因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以
,所以![]() ,
,
取![]() 的中点
的中点![]() ,连结
,连结![]() ,
,
由题设知四边形![]() 是等腰梯形,所以
是等腰梯形,所以![]() ,
,
由![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,所以
,所以![]() ,
,
建立如图所示空间直角坐标系,
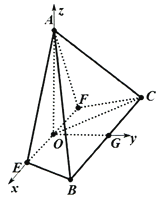
则![]() ,
, ![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则![]() ,即
,即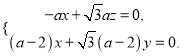
令![]() ,则
,则![]() ,于是
,于是![]() ,
,
又平面![]() 的一个法向量为
的一个法向量为![]() ,设二面角
,设二面角![]() 为
为![]() ,
,
所以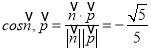 ,
, ![]() ,
,
所以二面角的正弦值为![]() .
.
(2)因为![]() 平面
平面![]() ,所以
,所以![]() ,即
,即![]() ,
,
因为![]() ,
,
所以![]() ,
,
由![]() 及
及![]() ,解得
,解得![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】园林管理处拟在公园某区域规划建设一半径为
 米圆心角为
米圆心角为 (弧度)的扇形景观水池,其中
(弧度)的扇形景观水池,其中 为扇形
为扇形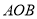 的圆心,同时紧贴水池周边建一圈理想的无宽度步道,要求总预算费用不超过
的圆心,同时紧贴水池周边建一圈理想的无宽度步道,要求总预算费用不超过 万元,水池造价为每平方米
万元,水池造价为每平方米 元,步道造价为每米
元,步道造价为每米 元.
元.(1)当
 和
和 分别为多少时,可使广场面积最大,并求出最大值;
分别为多少时,可使广场面积最大,并求出最大值;(2)若要求步道长为
 米,则可设计出水池最大面积是多少.
米,则可设计出水池最大面积是多少.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知椭圆
 的左顶点
的左顶点 ,且点
,且点 在椭圆上,
在椭圆上,  分别是椭圆的左、右焦点。过点
分别是椭圆的左、右焦点。过点 作斜率为
作斜率为 的直线交椭圆
的直线交椭圆 于另一点
于另一点 ,直线
,直线 交椭圆
交椭圆 于点
于点 .
.
(1)求椭圆
 的标准方程;
的标准方程;(2)若
 为等腰三角形,求点
为等腰三角形,求点 的坐标;
的坐标;(3)若
 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
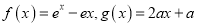 ,其中
,其中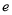 为自然对数的底数,
为自然对数的底数, 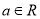 .
.(1)求证:
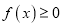 ;
;(2)若存在
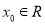 ,使
,使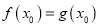 ,求
,求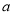 的取值范围;
的取值范围;(3)若对任意的
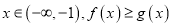 恒成立,求
恒成立,求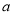 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 的焦点为
的焦点为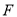 , 直线
, 直线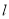 过点
过点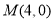 .
.(Ⅰ)若点
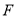 到直线
到直线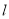 的距离为
的距离为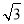 , 求直线
, 求直线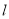 的斜率;
的斜率; (Ⅱ)设
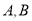 为抛物线上两点, 且
为抛物线上两点, 且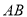 不与
不与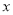 轴垂直, 若线段
轴垂直, 若线段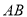 的垂直平分线恰过点
的垂直平分线恰过点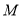 , 求证: 线段
, 求证: 线段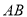 中点的横坐标为定值.
中点的横坐标为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某运输公司接受了向一地区每天至少运送180 t物资的任务,该公司有8辆载重为6 t的A型卡车和4辆载重为10 t的B型卡车,有10名驾驶员,每辆卡车每天往返的次数为A型卡车4次,B型卡车3次,每辆卡车每天往返的费用为A型卡车320元,B型卡车504元,则公司如何调配车辆,才能使公司所花的费用最低,最低费用为________元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆E:
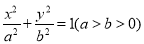 ,其焦点为F1,F2,离心率为
,其焦点为F1,F2,离心率为 ,直线l:x+2y-2=0与x轴,y轴分别交于点A,B,
,直线l:x+2y-2=0与x轴,y轴分别交于点A,B,(1)若点A是椭圆E的一个顶点,求椭圆的方程;
(2)若线段AB上存在点P满足|PF1|+|PF2|=2a,求a的取值范围.
相关试题

