
【题目】如图,在市中心有一矩形空地![]() .市政府欲将它改造成绿化景观带,具体方案如下:在边
.市政府欲将它改造成绿化景观带,具体方案如下:在边![]() 上分别取点M,N,在三角形
上分别取点M,N,在三角形![]() 内建造假山,在以
内建造假山,在以![]() 为直径的半圆内建造喷泉,其余区域栽种各种观赏类植物.
为直径的半圆内建造喷泉,其余区域栽种各种观赏类植物.
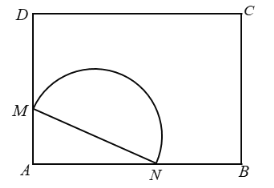
(1)若假山区域面积为![]() ,求喷泉区域面积的最小值;
,求喷泉区域面积的最小值;
(2)若![]() ,求假山区域面积的最大值.
,求假山区域面积的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)设![]() ,半圆的直径
,半圆的直径![]() ,根据假山区域面积为
,根据假山区域面积为![]() ,找到
,找到![]() 与
与![]() 的关系,再表示出喷泉区域面积,求最值,注意验证半圆是否在矩形空地
的关系,再表示出喷泉区域面积,求最值,注意验证半圆是否在矩形空地![]() 内,即验证是否能取到最小值;
内,即验证是否能取到最小值;
(2)由(1)根据以![]() 为直径的半圆区域在矩形广场内,求得
为直径的半圆区域在矩形广场内,求得![]() 的范围,再将假山区域面积用
的范围,再将假山区域面积用![]() 表示出来,再求最值.
表示出来,再求最值.
解:(1)设![]() ,半圆的直径
,半圆的直径![]() ,半圆的圆心为O.
,半圆的圆心为O.
在直角三角形![]() 中,
中,![]() ,所以
,所以![]() .
.
因为假山区域面积为![]() ,
,
所以![]()
所以![]() ,所以喷泉区域面积
,所以喷泉区域面积![]() ,
,
当且仅当![]() ,即
,即![]() 时取等号.此时
时取等号.此时![]() .
.
因为点O到![]() 的距离
的距离![]() ,点O到
,点O到![]() 的距离
的距离![]() ,
,
所以![]() ,即
,即![]() ,
,
![]() ,即
,即![]() .
.
所以以![]() 为直径的半圆区域一定在矩形广场内.
为直径的半圆区域一定在矩形广场内.
所以当![]() 时,
时,![]() 取得最小值
取得最小值![]() .
.
喷泉区域面积的最小值为![]() .
.
(2)由(1)知,若![]() ,则
,则![]() .
.
所以点O到![]() 的距离
的距离![]() ,
,
点O到![]() 的距离
的距离![]() ,
,
因为以![]() 为直径的半圆区域在矩形广场内,
为直径的半圆区域在矩形广场内,
所以![]() 即
即![]() 所以
所以![]() .
.
又因为![]() ,所以
,所以![]() .
.
所以假山区域面积![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以当![]() 时,假山区域面积的最大值为
时,假山区域面积的最大值为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图1,在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.现分别沿
的中点.现分别沿![]() ,
,![]() 将
将![]() 和
和![]() 折起,点
折起,点![]() 折至点
折至点![]() ,点
,点![]() 折至点
折至点![]() ,使得平面
,使得平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,连接
,连接![]() ,如图2.
,如图2.

(Ⅰ)若![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,求证:平面
的中点,求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求多面体![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() (
(![]() ,
,![]() ).
).
(1)若展开式中第5项与第7项的系数之比为3∶8,求k的值;
(2)设![]() (
(![]() ),且各项系数
),且各项系数![]() ,
,![]() ,
,![]() ,…,
,…,![]() 互不相同.现把这
互不相同.现把这![]() 个不同系数随机排成一个三角形数阵:第1列1个数,第2列2个数,…,第n列n个数.设
个不同系数随机排成一个三角形数阵:第1列1个数,第2列2个数,…,第n列n个数.设![]() 是第i列中的最小数,其中
是第i列中的最小数,其中![]() ,且i,
,且i,![]() .记
.记![]() 的概率为
的概率为![]() .求证:
.求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程:在平面直角坐标系![]() 中,曲线
中,曲线![]() :
:![]() (
(![]() 为参数),在以平面直角坐标系的原点为极点、
为参数),在以平面直角坐标系的原点为极点、![]() 轴的正半轴为极轴,且与平面直角坐标系
轴的正半轴为极轴,且与平面直角坐标系![]() 取相同单位长度的极坐标系中,曲线
取相同单位长度的极坐标系中,曲线![]() :
:![]() .
.
(1)求曲线![]() 的普通方程以及曲线
的普通方程以及曲线![]() 的平面直角坐标方程;
的平面直角坐标方程;
(2)若曲线![]() 上恰好存在三个不同的点到曲线
上恰好存在三个不同的点到曲线![]() 的距离相等,求这三个点的极坐标.
的距离相等,求这三个点的极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用一个平行于底面的截面去截一个正棱锥,截面和底面间的几何体叫正棱台.如图,在四棱台![]() 中,
中,![]() ,
,![]() 分别为
分别为![]() 的中点.
的中点.
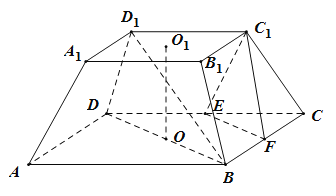
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)若侧棱所在直线与上下底面中心的连线![]() 所成的角为
所成的角为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成的角的余弦值.
所成的角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com