【题目】已知椭圆![]() 和抛物线
和抛物线![]() 有公共焦点
有公共焦点![]() ,
, ![]() 的中心和
的中心和![]() 的顶点都在坐标原点,过点
的顶点都在坐标原点,过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 分别相交于
分别相交于![]() 两点(其中点
两点(其中点![]() 在第四象限内).
在第四象限内).
(1)若![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)若坐标原点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 在抛物线
在抛物线![]() 上,直线
上,直线![]() 与椭圆
与椭圆![]() 有公共点,求椭圆
有公共点,求椭圆![]() 的长轴长的最小值.
的长轴长的最小值.
参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:
(1)利用题意设直线![]() 的方程为
的方程为![]() .设出点的坐标可求得
.设出点的坐标可求得 ![]() .则直线
.则直线![]() 的方程为
的方程为![]() .
.
(2)由题意可得直线的斜率存在,设出直线方程,由对称性联立直线与抛物线的方程可得椭圆![]() 的长轴长的最小值为
的长轴长的最小值为![]()
试题解析:
解:(1)解法一:由题意得抛物线方程为![]() .
.
设直线![]() 的方程为
的方程为![]() .
.
令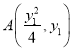 ,
, 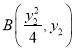 ,其中
,其中![]() . 由
. 由![]() ,得
,得![]() .
.
联立![]() ,可得
,可得![]() ,
,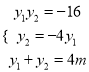 ,解得
,解得![]() ,
,![]() ,
,
![]()
![]() .
.
![]() 直线
直线![]() 的方程为
的方程为![]() .
.
(2)设![]() ,直线
,直线![]() ,
, ![]() 点
点![]() 在抛物线
在抛物线![]() 上,
上,
![]() 直线
直线![]() 的斜率存在,
的斜率存在, ![]()
![]() 关于直线
关于直线![]() 对称,所以
对称,所以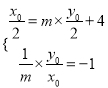 .解得
.解得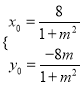 .
.
故![]() 代入抛物线
代入抛物线![]() ,可得
,可得![]() ,
, ![]() .
.
直线![]() 的方程为
的方程为![]() 或
或![]() .
.
设椭圆为![]() . 联立直线和椭圆,消去
. 联立直线和椭圆,消去![]() 整理得
整理得
![]()
![]()
![]()
![]()
![]() ,解得
,解得![]() .
.
则![]() ,即
,即![]() .
.![]() 椭圆
椭圆![]() 的长轴长的最小值为
的长轴长的最小值为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知侧棱垂直于底面的四棱柱
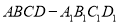 中,
中, 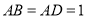 ,
, 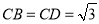 ,
, 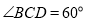 ,
, 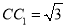 .
.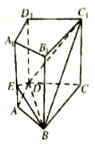
(1)若
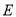 是线段
是线段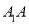 上的点且满足
上的点且满足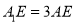 ,求证:平面
,求证:平面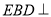 平面
平面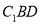 ;
;(2)求二面角
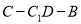 的平面角的余弦值.
的平面角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】平面内有向量
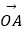 =(1,7),
=(1,7), 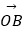 =(5,1),
=(5,1), 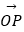 =(2,1),点X为直线OP上的一个动点.
=(2,1),点X为直线OP上的一个动点.
(1)当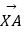
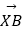 取最小值时,求
取最小值时,求 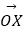 的坐标;
的坐标;
(2)当点X满足(1)的条件和结论时,求cos∠AXB的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,O为坐标原点,A、B、C三点满足
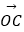 =
= 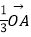 +
+ 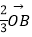 .
.
(1)求证:A、B、C三点共线;
(2)已知A(1,cosx)、B(1+sinx,cosx),x∈[0, ],f(x)=
],f(x)= 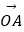
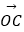 +(2m+
+(2m+  )|
)| 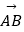 |+m2的最小值为5,求实数m的值.
|+m2的最小值为5,求实数m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某食品店为了了解气温对销售量的影响,随机记录了该店1月份中5天的日销售量
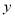 (单位:千克)与该地当日最低气温
(单位:千克)与该地当日最低气温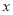 (单位:
(单位: 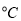 )的数据,如下表:
)的数据,如下表:x
2
5
8
9
11
y
12
10
8
8
7
(1)求出
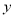 与
与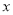 的回归方程
的回归方程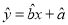 ;
;(2)判断
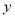 与
与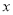 之间是正相关还是负相关;若该地1月份某天的最低气温为
之间是正相关还是负相关;若该地1月份某天的最低气温为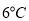 ,请用所求回归方程预测该店当日的销售量;
,请用所求回归方程预测该店当日的销售量;(3)设该地1月份的日最低气温
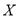 ~
~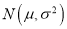 ,其中
,其中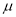 近似为样本平均数
近似为样本平均数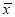 ,
, 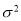 近似为样本方差
近似为样本方差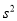 ,求
,求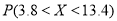 .
.附:①回归方程
 中,
中, 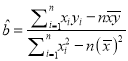 ,
, 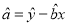 .
.②
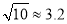 ,
, 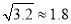 ,若
,若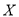 ~
~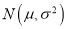 ,则
,则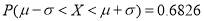 ,
, 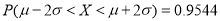 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,a,b,c分别是角A,B,C的对边,且a=80,b=100,A=
 ,则此三角形是( )
,则此三角形是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.锐角或钝角三角形 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an},{bn}满足a1=1,且an , an+1是函数f(x)=x2﹣bnx+2n的两个零点,则b10等于( )
A.24
B.32
C.48
D.64
相关试题

