【题目】如图,已知点![]() ,
,![]() ,抛物线
,抛物线![]() 的焦点
的焦点![]() 为线段
为线段![]() 中点.
中点.
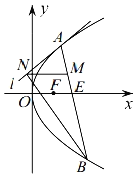
(1)求抛物线![]() 的方程;
的方程;
(2)过点![]() 的直线交抛物线
的直线交抛物线![]() 于
于![]() 两点,
两点,![]() ,过点
,过点![]() 作抛物线
作抛物线![]() 的切线
的切线![]() ,
,![]() 为切线
为切线![]() 上的点,且
上的点,且![]() 轴,求
轴,求![]() 面积的最小值.
面积的最小值.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
![]() 1
1![]() 由已知得焦点
由已知得焦点![]() ,所以
,所以![]() ,从而求出抛物线C的方程;
,从而求出抛物线C的方程;![]() 2
2![]() 设
设![]() ,
,![]() ,
,![]() ,设直线l方程为:
,设直线l方程为:![]() ,与抛物线方程联立,利用
,与抛物线方程联立,利用![]() 求得
求得![]() ,所以直线l的方程为:
,所以直线l的方程为:![]() ,由
,由![]() ,求得点M的坐标,进而求出点N的坐标,所以
,求得点M的坐标,进而求出点N的坐标,所以![]() 设直线AB的方程为:
设直线AB的方程为:![]() ,与抛物线方程联立,设直线l方程为:
,与抛物线方程联立,设直线l方程为:![]() ,利用韦达定理代入
,利用韦达定理代入![]() ,利用基本不等式即可求出
,利用基本不等式即可求出![]() 面积的最小值.
面积的最小值.
(1)由已知得焦点![]() 的坐标为
的坐标为![]() ,
,
![]() ,
,
![]() 抛物线
抛物线![]() 的方程为:
的方程为:![]() ;
;
(2)设直线![]() 的方程为:
的方程为:![]() ,设
,设![]() ,
,![]() ,
,![]() ,
,
联立方程![]() ,消去
,消去![]() 得:
得:![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
设直线![]() 方程为:
方程为:![]() ,
,
联立方程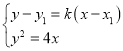 ,消去
,消去![]() 得:
得:![]() ,
,
由相切得:![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() 直线
直线![]() 的方程为:
的方程为:![]() ,
,
由![]() ,得
,得![]() ,
,![]() ,
,
将![]() 代入直线
代入直线![]() 方程,解得
方程,解得![]() ,
,
所以![]()
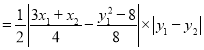
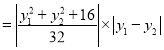
![]()
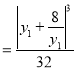 ,
,
又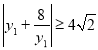 ,
,
所以![]() ,当且仅当
,当且仅当![]() 时,取到等号,
时,取到等号,
所以![]() 面积的最小值为
面积的最小值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
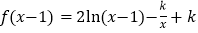 (
( ).
).(Ⅰ)判断当
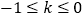 时
时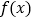 的单调性;
的单调性;(Ⅱ)若
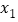 ,
,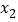 (
(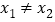 )为
)为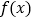 两个极值点,求证:
两个极值点,求证: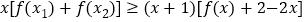 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,直线
中,直线 的参数方程为
的参数方程为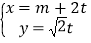 (
(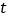 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,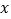 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线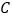 的极坐标方程为
的极坐标方程为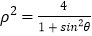 .
.(Ⅰ)求直线
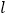 的普通方程和曲线
的普通方程和曲线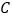 的直角坐标方程;
的直角坐标方程;(Ⅱ)设
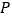 为曲线
为曲线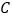 上的点,
上的点, ,垂足为
,垂足为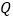 ,若
,若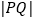 的最小值为
的最小值为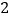 ,求
,求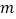 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某地区有3个不同值班地点,每个值班地点需配一名医务人员和两名警察,现将3名医务人员(1男2女)和6名警察(4男2女)分配到这3个地点去值班,要求每个值班地点至少有一名女性,则共有______种不同分配方案.(用具体数字作答)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
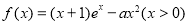 .
.(1)若函数
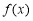 在
在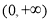 上单调递增,求实数
上单调递增,求实数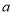 的取值范围;
的取值范围;(2)若函数
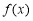 有两个不同的零点
有两个不同的零点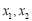 .
.(ⅰ)求实数
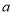 的取值范围;
的取值范围;(ⅱ)求证:
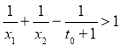 .(其中
.(其中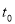 为
为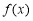 的极小值点)
的极小值点) -
科目: 来源: 题型:
查看答案和解析>>【题目】对于某种类型的口服药,口服
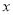 小时后,由消化系统进入血液中药物浓度
小时后,由消化系统进入血液中药物浓度 (单位)与时间
(单位)与时间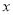 小时的关系为
小时的关系为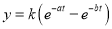 ,其中
,其中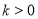 ,
,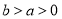 为常数,对于某一种药物
为常数,对于某一种药物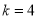 ,
,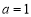 ,
,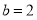 .
.(1)口服药物后______小时血液中药物浓度最高;
(2)这种药物服药
 小时后血液中药物浓度如下表
小时后血液中药物浓度如下表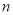
1
2
3
4
5
6
7
8
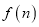
0.9545
0.9304
0.6932
0.4680
0.3010
0.1892
0.1163
0.072
一个病人上午8:00第一次服药,要使得病人血液中药物浓度保持在0.5个单位以上,第三次服药时间是______(时间以整点为准)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某圆柱的高为2,底面周长为16,其三视图如图所示,圆柱表面上的点
 在正视图上的对应点为
在正视图上的对应点为 ,圆柱表面上的点
,圆柱表面上的点 在左视图上的对应点为
在左视图上的对应点为 ,则在此圆柱侧面上,从
,则在此圆柱侧面上,从 到
到 的路径中,最短路径的长度为( )
的路径中,最短路径的长度为( )
A.
 B.
B.  C.
C.  D. 2
D. 2
相关试题

