搜索
【题目】如图所示，A是函数f（x）=2x的图象上的动点，过点A作直线平行于x轴，交函数g（x）=2x+2的图象于点B，若函数f（x）=2x的图象上存在点C使得△ABC为等边三角形，则称A为函数f（x）=2x上的好位置点．函数f（x）=2x上的好位置点的个数为（ ）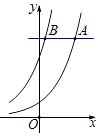 
A.0
B.1
C.2
D.大于2
参考答案：
【答案】B
【解析】解：根据题意，设A，B的纵坐标为m，
则A（log2m，m），B（log2m﹣2，m），
∴AB=log2m﹣log2m+2=2，
设C（x，2x），
∵△ABC是等边三角形，
∴点C到直线AB的距离为 
，
∴m﹣2x= ，
∴x=log2（m﹣ ），
∴x= 
（log2m+log2m﹣2）=log2m﹣1，
∴log2（m﹣ ）=log2m﹣1=log2 
，
∴m﹣ = ，
解得m=2 ，
∴x=log2（m﹣ ）=log2 ，
函数f（x）=2x上的好位置点的个数为1个，
故选：B．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知曲线C的极坐标方程是ρ=2cosθ，以极点为平面直角坐标系的原点，极轴为x轴的正半轴，建立平面直角坐标系，直线L的参数方程是
（t为参数）．
（1）求曲线C的直角坐标方程和直线L的普通方程；
（2）设点P（m，0），若直线L与曲线C交于A，B两点，且|PA||PB|=1，求实数m的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f（x）=alnx+bx（a，b∈R）在点（1，f（1））处的切线方程为x﹣2y﹣2=0．
（1）求a，b的值；
（2）当x＞1时，f（x）+
＜0恒成立，求实数k的取值范围；
（3）证明：当n∈N* ， 且n≥2时，
+ 
+…+ 
＞ 
． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f（x）=cos4x+sin2x，下列结论中错误的是（ ）
A.f（x）是偶函数
B.函f（x）最小值为
C.
是函f（x）的一个周期
D.函f（x）在（0， ）内是减函数 -
科目： 来源： 题型：
查看答案和解析>>【题目】设函数f（x）=
（a＞0，且a≠1）．
①若a=
，则函数f（x）的值域为；
②若f（x）在R上是增函数，则a的取值范围是 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f（x）的定义域为R．a，b∈R，若此函数同时满足：
①当a+b=0时，有f（a）+f（b）=0；
②当a+b＞0时，有f（a）+f（b）＞0，
则称函数f（x）为Ω函数．
在下列函数中：
①y=x+sinx；
②y=3x﹣（
）x；
③y=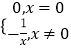
是Ω函数的为 ． （填出所有符合要求的函数序号） -
科目： 来源： 题型：
查看答案和解析>>【题目】已知抛物线
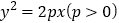的焦点为
，准线为
，过点的直线交拋物线于
，
两点，过点作准线的垂线，垂足为
，当点坐标为
时，
为正三角形，则此时
的面积为____________
相关试题
