【题目】已知函数![]() =lnx+ax2+(2a+1)x.
=lnx+ax2+(2a+1)x.
(1)讨论![]() 的单调性;
的单调性;
(2)当a﹤0时,证明![]() .
.
参考答案:
【答案】(1)见解析;(2)见解析.
【解析】试题分析:(1)先求函数导数![]() ,再根据导函数符号的变化情况讨论单调性:当
,再根据导函数符号的变化情况讨论单调性:当![]() 时,
时, ![]() ,则
,则![]() 在
在![]() 单调递增;当
单调递增;当![]() 时,
时, ![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减.(2)证明
单调递减.(2)证明![]() ,即证
,即证![]() ,而
,而![]() ,所以需证
,所以需证![]() ,设g(x)=lnx-x+1 ,利用导数易得
,设g(x)=lnx-x+1 ,利用导数易得![]() ,即得证.
,即得证.
试题解析:(1)f(x)的定义域为(0,+![]() ),
),![]() .
.
若a≥0,则当x∈(0,+![]() )时,
)时, ![]() ,故f(x)在(0,+
,故f(x)在(0,+![]() )单调递增.
)单调递增.
若a<0,则当x∈![]() 时,
时, ![]() ;当x∈
;当x∈![]() 时,
时, ![]() .故f(x)在
.故f(x)在![]() 单调递增,在
单调递增,在![]() 单调递减.
单调递减.
(2)由(1)知,当a<0时,f(x)在![]() 取得最大值,最大值为
取得最大值,最大值为
![]() .
.
所以![]() 等价于
等价于![]() ,即
,即![]() .
.
设g(x)=lnx-x+1,则![]() .
.
当x∈(0,1)时, ![]() ;当x∈(1,+
;当x∈(1,+![]() )时,
)时, ![]() .所以g(x)在(0,1)单调递增,在(1,+
.所以g(x)在(0,1)单调递增,在(1,+![]() )单调递减.故当x=1时,g(x)取得最大值,最大值为g(1)=0.所以当x>0时,g(x)≤0.从而当a<0时,
)单调递减.故当x=1时,g(x)取得最大值,最大值为g(1)=0.所以当x>0时,g(x)≤0.从而当a<0时, ![]() ,即
,即![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 是抛物线
是抛物线 :
:  (
( )上一点,
)上一点,  是抛物线的焦点,
是抛物线的焦点,  且
且 .
.(1)求抛物线
 的方程;
的方程;(2)已知
 ,过
,过 的直线
的直线 交抛物线
交抛物线 于
于 、
、 两点,以
两点,以 为圆心的圆
为圆心的圆 与直线
与直线 相切,试判断圆
相切,试判断圆 与直线
与直线 的位置关系,并证明你的结论.
的位置关系,并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分10分)已知等差数列{an}满足a1+a2=10,a4-a3=2.
(1)求{an}的通项公式.
(2)设等比数列{bn}满足b2=a3,b3=a7.问:b6与数列{an}的第几项相等?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二阶矩阵M有特征值λ=8及对应的一个特征向量
 =[
=[  ],并且矩阵M对应的变换将点(﹣1,2)变换成(﹣2,4).
],并且矩阵M对应的变换将点(﹣1,2)变换成(﹣2,4).
(1)求矩阵M;
(2)求矩阵M的另一个特征值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
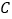 经过原点
经过原点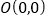 且与直线
且与直线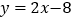 相切于点
相切于点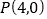
(Ⅰ)求圆
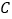 的方程;
的方程;(Ⅱ)在圆
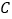 上是否存在两点
上是否存在两点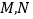 关于直线
关于直线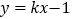 对称,且以线段
对称,且以线段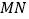 为直径的圆经过原点?若存在,写出直线
为直径的圆经过原点?若存在,写出直线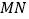 的方程;若不存在,请说明理由
的方程;若不存在,请说明理由 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,
中, ,
, ,
, ,平面
,平面 底面
底面 ,
, .
. 和
和 分别是
分别是 和
和 的中点,求证:
的中点,求证:
(Ⅰ)
 底面
底面 ;
;(Ⅱ)
 平面
平面 ;
;(Ⅲ)平面
 平面
平面 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知{an}为等差数列,前n项和为Sn(n∈N*),{bn}是首项为2的等比数列,且公比大于0,b2+b3=12,b3=a4-2a1,S11=11b4.
(Ⅰ)求{an}和{bn}的通项公式;
(Ⅱ)求数列{a2nbn}的前n项和(n∈N*).
相关试题

