【题目】已知函数![]() (
(![]() ,且
,且![]() ).
).
(1)求函数![]() 的单调区间;
的单调区间;
(2)若存在![]() ,使得
,使得![]() (
(![]() 是自然对数的底数),求实数
是自然对数的底数),求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)函数![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)先对![]() 求导,对
求导,对![]() 分情况讨论,都得到
分情况讨论,都得到![]() 在
在![]() 上是增函数,
上是增函数, ![]() ,∴
,∴![]() 的解集为
的解集为![]() ,
,![]() 的解集为
的解集为![]() ,得出函数
,得出函数![]() 的单调区间;(2)由已知条件得出
的单调区间;(2)由已知条件得出![]() ,转化成求函数
,转化成求函数![]() 的最值,分类讨论得出结果.
的最值,分类讨论得出结果.
试题解析:解:(1)![]()
∵当![]() 时,
时,![]() ,
,![]() 在
在![]() 上是增函数,
上是增函数,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上也是增函数,
上也是增函数,
∴当![]() 或
或![]() 时,总有
时,总有![]() 在
在![]() 上是增函数,
上是增函数,
又![]() ,∴
,∴![]() 的解集为
的解集为![]() ,
,![]() 的解集为
的解集为![]() ,
,
故函数![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() .
.
(2)∵存在![]() ,使得
,使得![]() 成立,
成立,
而当![]() 时,
时,![]() ,
,
∴只要![]() 即可.
即可.
又∵![]() ,
,![]() ,
,![]() 的变化情况如下表所示:
的变化情况如下表所示:
|
| 0 |
|
|
| 0 |
|
| 减函数 | 极小值 | 增函数 |
∴函数![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,
上是增函数,
∴当![]() 时,
时,![]() 的最小值
的最小值![]() ,
,
![]() 的最大值
的最大值![]() 为
为![]() 和
和![]() 中的最大者.
中的最大者.
∵![]() ,
,
令![]()
![]() ,
,
∵![]() ,∴
,∴![]() 在
在![]() 上是增函数.
上是增函数.
而![]() ,故当
,故当![]() 时,
时,![]() ,即
,即![]() ;
;
当![]() 时,
时,![]() ,即
,即![]() .
.
∴当![]() 时,
时,![]() ,即
,即![]() ,
,
函数![]() 在
在![]() 上是增函数,解得
上是增函数,解得![]() ;
;
当![]() 时,
时,![]() ,即
,即![]() ,
,
函数![]() 在
在![]() 上是减函数,解得
上是减函数,解得![]() .
.
综上所述,所求![]() 的取值范围为
的取值范围为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知双曲线
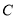 与椭圆
与椭圆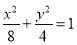 有相同的焦点,实半轴长为
有相同的焦点,实半轴长为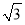 .
.(1)求双曲线
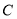 的方程;
的方程;(2)若直线
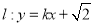 与双曲线
与双曲线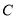 有两个不同的交点
有两个不同的交点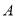 和
和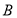 ,且
,且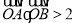 (其中
(其中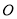 为原点),求
为原点),求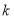 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P-ABCD中,四边形ABCD是矩形,侧面PAD⊥底面ABCD,若点E,F分别是PC,BD的中点。
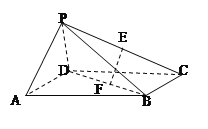
(1)求证:EF∥平面PAD;
(2)求证:平面PAD⊥平面PCD
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合
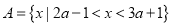 ,集合
,集合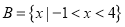 .
.(1)若
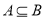 ,求实数
,求实数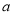 的取值范围;
的取值范围;(2)是否存在实数
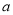 ,使
,使 ?若存在,求出
?若存在,求出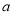 的值;若不存在,说明理由.
的值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
已知直线
 :
: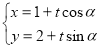 (
( 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,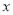 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线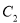 的极坐标方程为
的极坐标方程为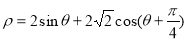 ,且
,且 与
与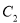 相交于
相交于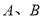 两点.
两点.(1)当
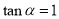 时,判断直线
时,判断直线 与曲线
与曲线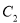 的位置关系,并说明理由;
的位置关系,并说明理由;(2)当
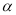 变化时,求弦
变化时,求弦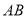 的中点
的中点 的普通方程,并说明它是什么曲线.
的普通方程,并说明它是什么曲线. -
科目: 来源: 题型:
查看答案和解析>>【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.
x
3
4
5
6
y
2.5
3
4
4.5
(1)请画出上表数据的散点图.
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程
 .
.(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤.
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图几何体
 是四棱锥,
是四棱锥,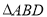 为正三角形,
为正三角形, ,
, ,
, ,且
,且 .
.
(1)求证:平面
 平面
平面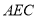 ;
;(2)
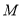 是棱
是棱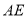 的中点,求证:
的中点,求证: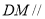 平面
平面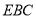 ;
;(3)求二面角
 的平面角的余弦值.
的平面角的余弦值.
相关试题

