【题目】已知函数![]()
(1)若a=1,求f(x)的极值;
(2)若存在x0∈[1,e],使得f(x0)<g(x0)成立,求实数a的取值范围.
参考答案:
【答案】(1)f(x)的极小值是f(1)=1,无极大值(2)![]()
【解析】分析:(1)求出导数![]() ,由不等式
,由不等式![]() 确定增区间,由
确定增区间,由![]() 确定减区间,从而得极值;
确定减区间,从而得极值;
(2)问题等价于![]() ,因此用导数研究函数
,因此用导数研究函数![]() 的最小值,由最小值小于0可求得
的最小值,由最小值小于0可求得![]() 的范围,注意要分类讨论.
的范围,注意要分类讨论.
详解:(1)a=1时,f(x)=x﹣lnx,函数f(x)的定义域是(0,+∞),
f′(x)=1﹣![]() =
=![]() ,令f′(x)>0,解得x>1,令f′(x)<0,解得:0<x<1,
,令f′(x)>0,解得x>1,令f′(x)<0,解得:0<x<1,
f(x)在(0,1)递减,在(1,+∞)递增,故f(x)的极小值是f(1)=1,无极大值;
(2)存在x0∈[1,e],使得f(x0)<g(x0)成立,等价于[f(x)﹣g(x)]min<0,
(x∈[1,e])成立,设h(x)=f(x)﹣g(x)=x﹣alnx+![]() ,
,
则h′(x)=![]() ,令h′(x)=0,解得:x=﹣1(舍),x=1+a;
,令h′(x)=0,解得:x=﹣1(舍),x=1+a;
①当1+a≥e,h(x)在[1,e]递减,∴h(x)min=h(e)=e2﹣ea+1+a,
令h(x)min<0,解得:a>![]() ;
;
②当1+a<e时,h(x)在(1,a+1)递减,在(a+1,e)递增,
∴h(x)min=h(1+a)=a[1﹣ln(a+1)]+2>2与h(x)min<0矛盾,
综上,a>![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
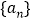 为等差数列,
为等差数列, ,
,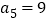 .
.(1) 求数列
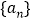 的通项公式;
的通项公式;(2)求数列
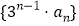 的前n项和
的前n项和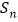 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】
 男
男 女共
女共 名同学从左至右排成一排合影,要求左端排男同学,右端排女同学,且女同学至多有
名同学从左至右排成一排合影,要求左端排男同学,右端排女同学,且女同学至多有 人排在一起,则不同的排法种数为( )
人排在一起,则不同的排法种数为( )A.
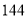 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数
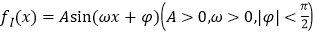 的一段图象过点
的一段图象过点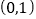 ,如图所示.
,如图所示.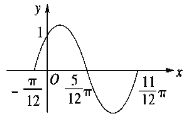
(1)求函数
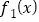 的表达式;
的表达式; (2)将函数
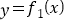 的图象向右平移
的图象向右平移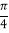 个单位,得函数
个单位,得函数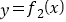 的图象,求
的图象,求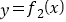 的最大值,并求出此时自变量
的最大值,并求出此时自变量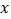 的集合,并写出该函数的增区间.
的集合,并写出该函数的增区间. -
科目: 来源: 题型:
查看答案和解析>>【题目】若函数f(x),g(x)满足
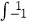 f(x)g(x)dx=0,则f(x),g(x)为区间[﹣1,1]上的一组正交函数,给出三组函数:
f(x)g(x)dx=0,则f(x),g(x)为区间[﹣1,1]上的一组正交函数,给出三组函数:
①f(x)=sin x,g(x)=cos
x,g(x)=cos  x;
x;
②f(x)=x+1,g(x)=x﹣1;
③f(x)=x,g(x)=x2 ,
其中为区间[﹣1,1]上的正交函数的组数是( )
A.0
B.1
C.2
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】由不等式组
 确定的平面区域记为Ω1 , 不等式组
确定的平面区域记为Ω1 , 不等式组 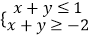 确定的平面区域记为Ω2 , 在Ω1中随机取一点,则该点恰好在Ω2内的概率为( )
确定的平面区域记为Ω2 , 在Ω1中随机取一点,则该点恰好在Ω2内的概率为( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某零售店近5个月的销售额和利润额资料如下表:
商店名称





销售额
 /千万元
/千万元3
5
6
7
9
利润额
 /百万元
/百万元2
3
3
4
5
(1)画出散点图.观察散点图,说明两个变量有怎样的相关关系;
(2)用最小二乘法计算利润额
 关于销售额
关于销售额 的回归直线方程;
的回归直线方程;(3)当销售额为4千万元时,利用(2)的结论估计该零售店的利润额(百万元).
[参考公式:
 ,
, ]
]
相关试题

