(12分)(2010·无锡模拟)已知f(x)在定义域(0,+∞)上为增函数,且满足f(xy)=f(x)+f(y),f(3)=1,试解不等式f(x)+f(x-8)≤2.
参考答案:
解 根据题意,由f(3)=1,得f(9)=f(3)+f(3)=2.
又f(x)+f(x-8)=f[x(x-8)],故f[x(x-8)]≤f(9).
∵f(x)在定义域(0,+∞)上为增函数,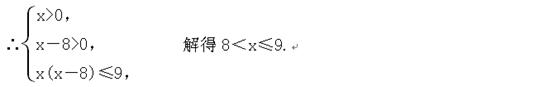
∴原不等式的解集为{x|8<x≤9}.
解析
-
科目: 来源: 题型:解答题
查看答案和解析>>(本小题13分)某饮料生产企业为了占有更多的市场份额,拟在2010年度进行
一系列促销活动,经过市场调查和测算,饮料的年销售量x万件与年促销费t万元间满足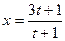 。已知2010年生产饮料的设备折旧
。已知2010年生产饮料的设备折旧 ,维修等固定费用为3 万元,每生产1万件
,维修等固定费用为3 万元,每生产1万件
饮料需再投入32万元的生产费用,若将每件饮料的售价定为:其生产成本的150%与平均
每件促销费的一半之和,则该年生产的饮料正好能销售完。
(1)将2010年的利润y(万元)表示为促销费t(万元)的函数;
(2)该企业2010年的促销费投入多少万元时,企业的年利润最大?
(注:利润=销售收入—生产 成本—促销费,生产成本=固定费用+生产费用)
成本—促销费,生产成本=固定费用+生产费用) -
科目: 来源: 题型:解答题
查看答案和解析>>(本小题满分14分)已知
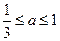 ,若函数
,若函数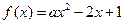 在区间
在区间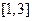 上
上
的最大值为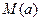 ,最小值为
,最小值为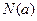 ,令
,令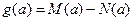 .
.
(1)求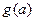 的函数表达式;
的函数表达式;
(2)判断函数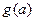 在区间
在区间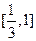 上的单调性,并求出
上的单调性,并求出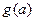 的最小值.
的最小值. -
科目: 来源: 题型:解答题
查看答案和解析>>(13分)已知函数f(x)=ax+
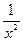 (x≠0,常数a∈R).
(x≠0,常数a∈R).
(1)讨论函数f(x)的奇偶性,并说明理由;
(2)若函数f(x)在x∈[3,+∞)上为增函数,求a的取值范围. -
科目: 来源: 题型:解答题
查看答案和解析>>(14分)某公司生产一种产品的固定成本为0.5万元,但每生产100件需再增加成本0.25万元,市场对此产品的年需求量为500件,年销售收入(单位:万元)为R(t)=5t-
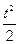 (0≤t≤5),其中t为产品售出的数量(单位:百件).
(0≤t≤5),其中t为产品售出的数量(单位:百件).
(1)把年利润表示为年产量x(百件)(x≥0)的函数f(x);
(2)当年产量为多少件时,公司可获得最大年利润? -
科目: 来源: 题型:解答题
查看答案和解析>>(本小题满分12分)
(1)判断函数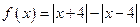 的奇偶性;
的奇偶性;
( 2)若
2)若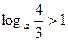 ,求a的取值范围.
,求a的取值范围. -
科目: 来源: 题型:解答题
查看答案和解析>>已知函数
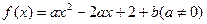 ,在区间
,在区间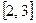 上有最大值5,最小
上有最大值5,最小
值2。
(1)求a,b的值。
(2)若 上单调,求
上单调,求 的取值范围。
的取值范围。
相关试题

