【题目】近年来，随着“雾霾”天出现的越来越频繁，很多人为了自己的健康，外出时选择戴口罩，长郡中学高三兴趣研究小组利用暑假空闲期间做了一项对人们雾霾天外出时是否戴口罩的调查，共调查了120人，其中女性70人，男性50人，并根据统计数据画出等高条形图如图所示：
（Ⅰ）利用图形判断性别与雾霾天外出戴口罩是否有关系；
（Ⅱ）根据统计数据建立一个
列联表；
（Ⅲ）能否在犯错误的概率不超过0.05的前提下认为性别与雾霾天外出戴口罩有关系.
附：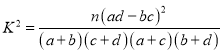
【答案】（1）性别与雾霾天外出戴口罩有关系（2）见解析（2）在犯错误的概率不超过0.05的前提下认为性别与雾霾天外出戴口罩有关系.
【解析】
试题（1）女性中雾霾天外出戴口罩的频率明显高于男性中雾霾天外出戴口罩的频率，因此可以认为性别与雾霾天外出戴口罩有关系.（2）根据数据依次填表即可（3）根据卡方公式求
，再与参考数据比较得结论
试题解析：解：（Ⅰ）在等高条形图中，两个深颜色条的高分别表示女性和男性中雾霾天外出戴口罩的频率，比较图中两个深颜色条的高可以发现，女性中雾霾天外出戴口罩的频率明显高于男性中雾霾天外出戴口罩的频率，因此可以认为性别与雾霾天外出戴口罩有关系.
（Ⅱ）
列联表如下：
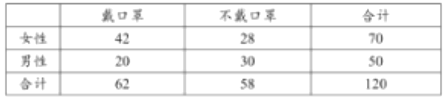
（Ⅲ）由（Ⅱ）中数据得：
.
所以，在犯错误的概率不超过0.05的前提下认为性别与雾霾天外出戴口罩有关系.
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案科目：高中数学 来源： 题型：
【题目】甲、乙两人各进行3次投篮，甲每次投中目标的概率为
，乙每次投中目标的概率为
，假设两人投篮是否投中相互之间没有影响，每次投篮是否投中相互之间也没有影响。
（1）求甲至少有一次未投中目标的概率；
（2）记甲投中目标的次数为
，求的概率分布及数学期望；
（3）求甲恰好比乙多投中目标2次的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程，下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况. 下列叙述中正确的是（ ）
A. 消耗1升汽油，乙车最多可行驶5千米
B. 以相同速度行驶相同路程，三辆车中，甲车消耗汽油最多
C. 甲车以80千米/小时的速度行驶1小时，消耗10升汽油
D. 某城市机动车最高限速80千米/小时. 相同条件下，在该市用丙车比用乙车更省油
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在极坐标系中，曲线
,曲线
．以极点为坐标原点，极轴为
轴正半轴建立平面直角坐标系
，曲线
的参数方程为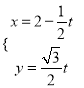
（
为参数）．
（1）求
的直角坐标方程；
（2）
与
交于不同的四点，这四点在
上排列顺次为
,求
的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某公司设计如图所示的环状绿化景观带，该景观带的内圈由两条平行线段（图中的
)和两个半圆构成，设
，且
.
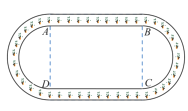
（1）若内圈周长为
，则
取何值时，矩形
的面积最大？
（2）若景观带的内圈所围成区域的面积为
，则取何值时，内圈周长最小？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】(本小题满分12分)
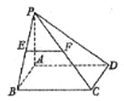
如图，在四棱锥P—ABCD中，底面ABCD是矩形，PA⊥平面ABCD，AP=AB，BP=BC=2，E，F分别是PB,PC的中点.
(Ⅰ)证明：EF∥平面PAD；
(Ⅱ)求三棱锥E—ABC的体积V.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列说法中正确的是（ ）
A. “
”是“
”成立的充分不必要条件
B. 命题
，则
C. 为了了解800名学生对学校某项教改试验的意见，用系统抽样的方法从中抽取一个容量为40的样本，则分组的组距为40
D. 已知回归直线的斜率的估计值为1.23，样本点的中心为
，则回归直线方程为
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
