【题目】甲、乙两人各进行3次投篮，甲每次投中目标的概率为，乙每次投中目标的概率为，假设两人投篮是否投中相互之间没有影响，每次投篮是否投中相互之间也没有影响。

（1）求甲至少有一次未投中目标的概率；

（2）记甲投中目标的次数为，求的概率分布及数学期望；

（3）求甲恰好比乙多投中目标2次的概率.

【答案】（1）（2）见解析（3）

【解析】

(1)利用对立事件公式可得满足题意的概率值；

(2)首先由超几何分布概率公式可得满足题意的概率值，然后求解其分布列和数学期望即可；

(3)由题意利用独立事件概率公式可得甲恰好比乙多投中目标2次的概率.

（1）记“甲连续投篮3次，至少1次未投中目标”为事件，

由题意知两人投篮是否投中目标，相互之间没有影响，投篮3次，相当于3次独立重复试验，

故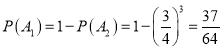，故甲至少有1次未投中目标的概率为；

（2）由题意知的可能取值是0，1，2，3，

，

，

，

，

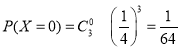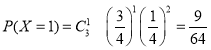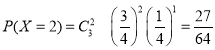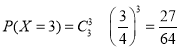的概率分别如下表：

0

1

2

3

；

（3）设甲恰比乙多投中目标2次为事件，甲恰投中目标2次且乙恰投中目标0次为事件，甲恰投中目标3次且乙恰投中目标1次为事件，则为互斥事件.

∴甲恰好比乙多投中目标2次的概率为。

关闭