
【题目】已知函数f(x)=|3x+2|.
(1)解不等式f(x)<4-|x-1|;
(2)已知m+n=1(m,n>0),若|x-a|-f(x)≤![]() (a>0)恒成立,求实数a的取值范围.
(a>0)恒成立,求实数a的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)利用零点分段法分类讨论解绝对值不等式即可.
(2)利用基本不等式求出![]() 的最小值,令g(x)=|x-a|-f(x)=|x-a|-|3x+2|,只需g(x)max
的最小值,令g(x)=|x-a|-f(x)=|x-a|-|3x+2|,只需g(x)max![]() 即可求解.
即可求解.
(1)不等式f(x)<4-|x-1|,即|3x+2|+|x-1|<4.
当x<-![]() 时,即-3x-2-x+1<4,
时,即-3x-2-x+1<4,
解得-![]() <x<-
<x<-![]() ;
;
当-![]() ≤x≤1时,即3x+2-x+1<4,
≤x≤1时,即3x+2-x+1<4,
解得-![]() ≤x<
≤x<![]() ;
;
当x>1时,即3x+2+x-1<4,无解.
综上所述,不等式的解集为![]() .
.
(2) ![]() =
=![]() (m+n)=1+1+
(m+n)=1+1+![]()
![]() ,
,
当且仅当![]() 时取等号,
时取等号,
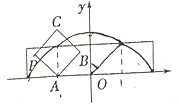
令g(x)=|x-a|-f(x)=|x-a|-|3x+2|=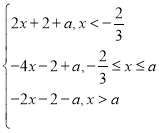 ,
,
所以当x=-![]() 时,g(x)max=
时,g(x)max=![]() +a,要使不等式恒成立,
+a,要使不等式恒成立,
只需g(x)max=![]() +a≤4,即0<a≤
+a≤4,即0<a≤![]()
.故实数a的取值范围为![]() .
.


 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,上顶点为
,上顶点为![]() ,过点
,过点![]() 与
与![]() 垂直的直线交
垂直的直线交![]() 轴负半轴于点
轴负半轴于点![]() ,且
,且![]() ,过
,过![]() ,
,![]() 三点的圆恰好与直线
三点的圆恰好与直线![]() 相切.
相切.
![]() 求椭圆
求椭圆![]() 的方程;
的方程;
![]() 过右焦点
过右焦点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,问在
两点,问在![]() 轴上是否存在点
轴上是否存在点![]() ,使得以
,使得以![]() 为邻边的平行四边形是菱形?如果存在,求出
为邻边的平行四边形是菱形?如果存在,求出![]() 的取值范围;如果不存在,说明理由.
的取值范围;如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两人作游戏,甲先在纸上任意写下一个由L、R构成的长为![]() 的序列,然后乙将
的序列,然后乙将![]() 个质量互不相同的砝码逐一放在天平上,每放一个砝码(已放的砝码不再拿下),乙都在纸上按顺序写一个字母:如果天平倾向左边则写L,否则写R.当所有砝码都放在天平上时,乙也写下一个由L、R构成的长为
个质量互不相同的砝码逐一放在天平上,每放一个砝码(已放的砝码不再拿下),乙都在纸上按顺序写一个字母:如果天平倾向左边则写L,否则写R.当所有砝码都放在天平上时,乙也写下一个由L、R构成的长为![]() 的序列.规定:当乙写的序列与甲写的序列相同时乙胜,否则甲胜.试问:谁有必胜策略?
的序列.规定:当乙写的序列与甲写的序列相同时乙胜,否则甲胜.试问:谁有必胜策略?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某综艺节目为比较甲、乙两名选手的各项能力(指标值满分为5分,分值高者为优),分别绘制了如图所示的六维能力雷达图,图中点A表示甲的创造力指标值为4,点B表示乙的空间能力指标值为3,则下列叙述错误的是( )
A.甲的六大能力中推理能力最差B.甲的创造力优于观察能力
C.乙的计算能力优于甲的计算能力D.乙的六大能力整体水平低于甲
查看答案和解析>>
科目:高中数学 来源: 题型:
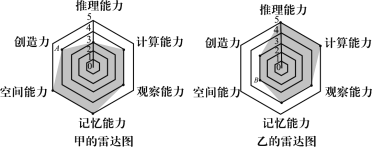
【题目】如图,四边形ABCD为矩形,沿AB将△ADC翻折成![]() .设二面角
.设二面角![]() 的平面角为
的平面角为![]() ,直线
,直线![]() 与直线BC所成角为
与直线BC所成角为![]() ,直线
,直线![]() 与平面ABC所成角为
与平面ABC所成角为![]() ,当
,当![]() 为锐角时,有
为锐角时,有
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
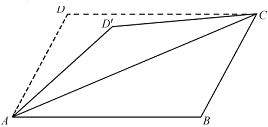
【题目】如图放置的边长为1的正方形![]() 沿
沿![]() 轴滚动,点
轴滚动,点![]() 恰好经过原点.设顶点
恰好经过原点.设顶点![]() 的轨迹方程是
的轨迹方程是![]() ,则对函数
,则对函数![]() 有下列判断:①函数
有下列判断:①函数![]() 是偶函数;②对任意的
是偶函数;②对任意的![]() ,都有
,都有![]() ;③函数
;③函数![]() 在区间
在区间![]() 上单调递减;④函数
上单调递减;④函数![]() 的值域是
的值域是![]() ;⑤
;⑤![]() .其中判断正确的序号是__________.
.其中判断正确的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司印制了一批文化衫,每件文化衫可有红、黄、蓝三种不同的颜色和四种不同的图案.现将这批文化衫分发给![]() 名新员工,每名员工恰好分到图案不同的4件.试求
名新员工,每名员工恰好分到图案不同的4件.试求![]() 的最小值,使得总存在两个人,他们所分到的某两种图案的4件文化衫的颜色全部相同.
的最小值,使得总存在两个人,他们所分到的某两种图案的4件文化衫的颜色全部相同.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com