【题目】设椭圆的左、右焦点分别为，，上顶点为，过点与垂直的直线交轴负半轴于点，且，过，三点的圆恰好与直线相切．

求椭圆的方程；

过右焦点作斜率为的直线与椭圆交于两点，问在轴上是否存在点，使得以为邻边的平行四边形是菱形？如果存在，求出的取值范围；如果不存在，说明理由．

【答案】（1） ；（2）存在， .

【解析】

设点的坐标为，且，利用以及得出点的坐标，利用外接圆圆心到该直线的距离等于半径，可求出的值，进而得出与的值，从而得出椭圆的方程；令，得出，设点、，将直线l的方程与椭圆的方程联立，利用韦达定理，求出线段的中点的坐标，将条件“以为邻边的平行四边形是菱形”转化为，得出这两条直线的斜率之积为，然后得出的表达式，利用不等式的性质可求出实数的取值范围．

设椭圆C的焦距为，则点的坐标为，点的坐标为，设点Q的坐标为，且，

如下图所示，

，，

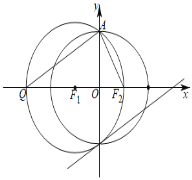
，则，所以，，则点Q的坐标为，

直线与直线AQ垂直，且点，所以，，，

由，得，则，．

为直角三角形，且为斜边，

线段的中点为，的外接圆半径为2c．

由题意可知，点到直线的距离为，

所以，，，，

因此，椭圆C的方程为.

由题意知，直线的斜率，并设，则直线l的方程为，

设点、

将直线的方程与椭圆C的方程联立，

消去x得，

由韦达定理得，．

，．

所以，线段MN的中点为点．

由于以PM，PN为邻边的平行四边形是菱形，则，则，所以，．

由两点连线的斜率公式可得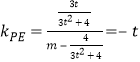，得．

由于，则，所以，，所以，．

因此，在x轴上存在点，使得以PM，PN为邻边的平行四边形是菱形，

且实数m的取值范围是．

关闭