【题目】某工厂新购置甲、乙两种设备，分别生产A，B两种产品，为了解这两种产品的质量，随机抽取了200件进行质量检测，得到质量指标值的频数统计表如下：
质量指标值 |
|
|
|
|
|
| 合计 |
A产品频数 | 2 | 6 | a | 32 | 20 | 10 | 80 |
B产品频数 | 12 | 24 | b | 27 | 15 | 6 | n |
产品质量2×2列联表
产品质量高 | 产品质量一般 | 合计 | |
A产品 | |||
B产品 | |||
合计 |
附：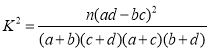
|
|
|
|
|
|
|
|
（1）求a，b，n的值，并估计A产品质量指标值的平均数；
（2）若质量指标值大于50，则说明该产品质量高，否则说明该产品质量一般.请根据频数表完成
列联表，并判断是否有
的把握认为质量高低与引入甲、乙设备有关.
科目：高中数学 来源： 题型：
【题目】已知椭圆
：
和圆
：
，
，
为椭圆的左、右焦点，点
在椭圆上，当直线
与圆相切时，
.
（Ⅰ）求的方程；
（Ⅱ）直线
：
与
轴交于点
，且与椭圆和圆都相切，切点分别为
，
，记
和
的积分别为
和
，求
的最小值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在直角坐标系
中，曲线
的参数方程为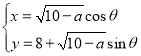
（
为参数，常数
）.以坐标原点为极点，
轴的正半轴为极轴建立极坐标系，已知直线
的极坐标方程为
.
（1）写出
及直线的直角坐标方程，并指出是什么曲线；
（2）设
是曲线上的一个动点，求点到直线的距离的最小值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某公司为了对某种商品进行合理定价，需了解该商品的月销售量
（单位：万件）与月销售单价
（单位：元/件）之间的关系，对近
个月的月销售量
和月销售单价
数据进行了统计分析，得到一组检测数据如表所示：
月销售单价 |
|
|
|
|
|
|
月销售量 |
|
|
|
|
|
|
（1）若用线性回归模型拟合与之间的关系，现有甲、乙、丙三位实习员工求得回归直线方程分别为：
，
和
，其中有且仅有一位实习员工的计算结果是正确的．请结合统计学的相关知识，判断哪位实习员工的计算结果是正确的，并说明理由；
（2）若用
模型拟合与之间的关系，可得回归方程为
，经计算该模型和（1）中正确的线性回归模型的相关指数
分别为
和
，请用说明哪个回归模型的拟合效果更好；
（3）已知该商品的月销售额为
（单位：万元），利用（2）中的结果回答问题：当月销售单价为何值时，商品的月销售额预报值最大？（精确到
）
参考数据：
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知四棱锥
，底面
为菱形， 
,H为
上的点，过
的平面分别交
于点
，且
平面
．
（1）证明： 
；
（2）当
为的中点， 
，
与平面所成的角为
，求二面角
的余弦值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
