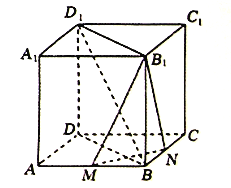
【题目】若图,在正方体![]() 中,
中, ![]() 分别是
分别是![]() 的中点.
的中点.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)在棱![]() 上是存在一点
上是存在一点![]() ,使得
,使得![]() 平面
平面![]() ,若存在,求
,若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
参考答案:
【答案】(1)证明过程见解析;(2) ![]()
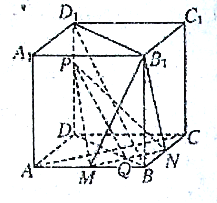
【解析】试题分析:(1)连接![]() ,由正方形性质得
,由正方形性质得![]() ,又由正方体
,又由正方体![]() 中,
中, ![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点,易得
的中点,易得![]() ,则
,则![]() ,
, ![]() ,由线面垂直的判定定理,可得
,由线面垂直的判定定理,可得![]() 平面
平面![]() ,进而由面面垂直的判定定理,可得平面
,进而由面面垂直的判定定理,可得平面![]() 平面
平面![]() ;(2)设
;(2)设![]() 与
与![]() 的交点是
的交点是![]() ,连接
,连接![]() ,
, ![]() ,
, ![]() ,由线面平行的性质定理,我们易由
,由线面平行的性质定理,我们易由![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,得
,得![]() ,再由平行线分线段成比例定理,得到线段
,再由平行线分线段成比例定理,得到线段![]() 与
与![]() 的比.
的比.
试题解析:(1)证明:连接![]() ,则
,则![]() ,又
,又![]() 分别是
分别是![]() 的中点,
的中点,
所以![]() ,所以
,所以![]() ,因为
,因为![]() 是正方体,
是正方体,
所以![]() 平面
平面![]() ,因为
,因为![]() 平面
平面![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() 平面
平面![]() 。
。
(2)设![]() 与
与![]() 的交点是
的交点是![]() ,连接
,连接![]() ,
,
因为![]() 平面
平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校高三(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,可见部分如下:

试根据图表中的信息解答下列问题:
(1)求全班的学生人数及分数在[70,80)之间的频数;
(2)为快速了解学生的答题情况,老师按分层抽样的方法从位于[70,80),[80,90)和[90,100]分数段的试卷中抽取8份进行分析,再从中任选3人进行交流,求交流的学生中,成绩位于[70,80)分数段的人数X的分布列和数学期望.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 的顶点
的顶点 边上的中线
边上的中线 所在直线方程为
所在直线方程为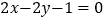 ,
,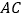 边上的高所在直线的方程为
边上的高所在直线的方程为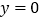 .
.(1)求
 的顶点
的顶点 的坐标;
的坐标;(2)若圆
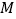 经过不同三点
经过不同三点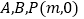 ,且斜率为
,且斜率为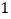 的直线与圆
的直线与圆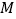 相切与点
相切与点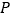 ,求圆的方程
,求圆的方程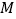 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
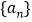 的前
的前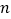 项和
项和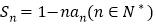 .
.(1)计算
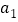 ,
,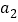 ,
,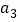 ,
, ;
;(2)猜想
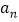 的表达式,并用数学归纳法证明你的结论.
的表达式,并用数学归纳法证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】7人站成一排.(写出必要的过程,结果用数字作答)
(1)甲、乙两人相邻的排法有多少种?
(2)甲、乙两人不相邻的排法有多少种?
(3)甲、乙、丙三人两两不相邻的排法有多少种?
(4)甲、乙、丙三人至多两人不相邻的排法有多少种?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
 ,底面
,底面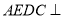 侧面
侧面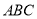 ,
,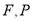 分别为
分别为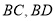 的中点,且
的中点,且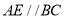 ,
,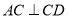 ,
, ,
,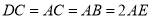 .
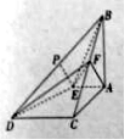
.
(I)证明:
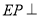 平面
平面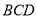 ;
;(II)设
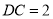 ,求三棱锥
,求三棱锥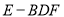 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
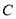 的方程
的方程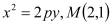 为抛物线
为抛物线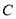 上一点,
上一点,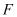 为抛物线的焦点.
为抛物线的焦点.(I)求
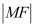 ;
;(II)设直线
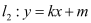 与抛物线
与抛物线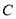 有唯一公共点
有唯一公共点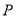 ,且与直线
,且与直线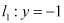 相交于点
相交于点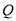 ,试问,在坐标平面内是否存在点
,试问,在坐标平面内是否存在点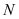 ,使得以
,使得以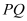 为直径的圆恒过点
为直径的圆恒过点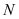 ?若存在,求出点
?若存在,求出点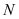 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
相关试题

