【题目】已知![]() 的顶点
的顶点![]() 边上的中线
边上的中线![]() 所在直线方程为
所在直线方程为![]() ,
,![]() 边上的高所在直线的方程为
边上的高所在直线的方程为![]() .
.
(1)求![]() 的顶点
的顶点![]() 的坐标;
的坐标;
(2)若圆![]() 经过不同三点
经过不同三点![]() ,且斜率为
,且斜率为![]() 的直线与圆
的直线与圆![]() 相切与点
相切与点![]() ,求圆的方程
,求圆的方程![]() .
.
参考答案:
【答案】(1)![]() ,
,![]() ; (2)圆方程为
; (2)圆方程为![]()
【解析】试题分析:(1)依题意知,点C是直线x=0和![]() 的交点,从而得出点C的坐标;设出点B的坐标由AB的中点在直线CD上求出点B的坐标.(2)线段AB和线段BP是圆的两条弦,所以两条弦的中垂线交点为圆心M坐标,即用m表示圆心M坐标,然后利用点P处的切线的斜率为1,可知
的交点,从而得出点C的坐标;设出点B的坐标由AB的中点在直线CD上求出点B的坐标.(2)线段AB和线段BP是圆的两条弦,所以两条弦的中垂线交点为圆心M坐标,即用m表示圆心M坐标,然后利用点P处的切线的斜率为1,可知![]() ,从而求出m的值,进而求出圆的方程.
,从而求出m的值,进而求出圆的方程.
试题解析:(1)![]() 边上的高
边上的高![]() 所在直线的方程为
所在直线的方程为![]() ,所以,
,所以,![]() ,
,
又![]() ,所以,
,所以,![]() ,
,
设![]() ,则
,则![]() 的中点
的中点![]() ,代入方程
,代入方程![]() ,
,
解得![]() ,所以
,所以![]() .
.
(2)由![]() ,
,![]() 可得,圆
可得,圆![]() 的弦
的弦![]() 的中垂线方程为
的中垂线方程为![]() ,
,
注意到![]() 也是圆
也是圆![]() 的弦,所以,圆心在直线
的弦,所以,圆心在直线![]() 上,
上,
设圆心![]() 坐标为
坐标为![]() ,
,
因为圆心![]() 在直线
在直线![]() 上,所以
上,所以![]() ①,
①,
又因为斜率为![]() 的直线与圆
的直线与圆![]() 相切于点
相切于点![]() ,所以
,所以![]() ,
,
即![]() ,整理得
,整理得![]() ②,
②,
由①②解得![]() ,
,![]() ,
,
所以,![]() ,半径
,半径![]() ,
,
所以所求圆方程为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱
 中,
中,  是边长为4的正方形.平面
是边长为4的正方形.平面 ⊥平面
⊥平面 ,
,  .
.(1)求证:
 ⊥平面ABC;
⊥平面ABC;(2)求二面角
 的余弦值;
的余弦值;(3)证明:在线段
 存在点
存在点 ,使得
,使得 ,并求
,并求 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场举行有奖促销活动,顾客购买一定金额商品后即可抽奖,每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖;若只有1个红球,则获二等奖;若没有红球,则不获奖.
(1)求顾客抽奖1次能获奖的概率;
(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为
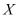 ,求
,求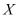 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校高三(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,可见部分如下:

试根据图表中的信息解答下列问题:
(1)求全班的学生人数及分数在[70,80)之间的频数;
(2)为快速了解学生的答题情况,老师按分层抽样的方法从位于[70,80),[80,90)和[90,100]分数段的试卷中抽取8份进行分析,再从中任选3人进行交流,求交流的学生中,成绩位于[70,80)分数段的人数X的分布列和数学期望.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
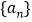 的前
的前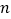 项和
项和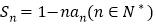 .
.(1)计算
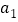 ,
,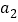 ,
,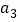 ,
, ;
;(2)猜想
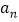 的表达式,并用数学归纳法证明你的结论.
的表达式,并用数学归纳法证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】若图,在正方体
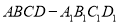 中,
中, 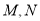 分别是
分别是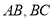 的中点.
的中点.(1)求证:平面
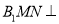 平面
平面 ;
;(2)在棱
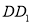 上是存在一点
上是存在一点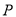 ,使得
,使得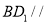 平面
平面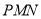 ,若存在,求
,若存在,求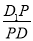 的值;若不存在,说明理由.
的值;若不存在,说明理由.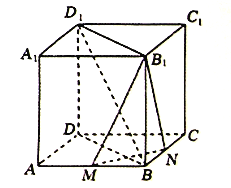
-
科目: 来源: 题型:
查看答案和解析>>【题目】7人站成一排.(写出必要的过程,结果用数字作答)
(1)甲、乙两人相邻的排法有多少种?
(2)甲、乙两人不相邻的排法有多少种?
(3)甲、乙、丙三人两两不相邻的排法有多少种?
(4)甲、乙、丙三人至多两人不相邻的排法有多少种?
相关试题

