【题目】海南省椰树集团引进德国净水设备的使用年限(年)和所需要的维修费用y(千元)的几组统计数据如表:
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(1)请根据上表提供的数据,用最小二乘法求出 ![]() 关于x的线性回归方程
关于x的线性回归方程 ![]() ;
;
(2)我们把中(1)的线性回归方程记作模型一,观察散点图发现该组数据也可以用函数模型 ![]() =c1ln(c2x)拟合,记作模型二.经计算模型二的相关指数R2=0.64,
=c1ln(c2x)拟合,记作模型二.经计算模型二的相关指数R2=0.64,
①请说明R2=0.64这一数据在线性回归模型中的实际意义.
②计算模型一中的R2的值(精确到0.01),通过数据说明,两种模型中哪种模型的拟合效果好.
参考公式和数值:用最小工乘法求线性回归方程系数公式 ![]() =
=  ,
, ![]() .R2=1﹣
.R2=1﹣  ,
, ![]() =0.651,(2×2.2+3×3.8+4×5.5+5×6.5+6×7.0=112.3)
=0.651,(2×2.2+3×3.8+4×5.5+5×6.5+6×7.0=112.3)
参考答案:
【答案】
(1)解:∵ ![]() ,且
,且 ![]() ,∴
,∴ ![]()
![]()
∴回归直线为 ![]() .
.
(2)解:①R2=0.64表明“净水设备的使用年限解释了64%的维修费用的变化”,或者说“净水设备的维修费用
的差异有64%是由净水设备的使用年限引起的”
② ![]() ,
, ![]() ,
, 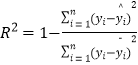 =0.96R2
=0.96R2
取值越大,意味着残差平方和越小,也就是说模型的拟合效果越好.
由于模型一中的相关指数R2=0.96大于0.64,说明模型一的拟合效果好
【解析】(1)先做出两组数据的平均数,把平均数和条件中所给的两组数据代入求解b的公式,做出b的值,再求出a的值,写出回归直线的方程.(2)①R2=0.64表明“净水设备的使用年限解释了64%的维修费用的变化”,或者说“净水设备的维修费用的差异有64%是由净水设备的使用年限引起的”②R2取值越大,意味着残差平方和越小,也就是说模型的拟合效果越好.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2﹣2ax+a在区间(1,3)内有极小值,则函数g(x)=
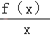 在区间(1,+∝)上一定( )
在区间(1,+∝)上一定( )
A.有最小值
B.有最大值
C.是减函数
D.是增函数 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆的左焦点为F1有一小球A 从F1处以速度v开始沿直线运动,经椭圆壁反射(无论经过几次反射速度大小始终保持不变,小球半径忽略不计),若小球第一次回到F1时,它所用的最长时间是最短时间的5倍,则椭圆的离心率为( )
A.
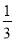 B.
B. 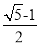 C.
C. 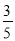 D.
D. 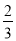
-
科目: 来源: 题型:
查看答案和解析>>【题目】设甲、乙、丙三人进行围棋比赛,每局两人参加,没有平局.在一局比赛中,甲胜乙的概率为
 ,甲胜丙的概率为
,甲胜丙的概率为  ,乙胜丙的概率为
,乙胜丙的概率为  .比赛顺序为:首先由甲和乙进行第一局的比赛,再由获胜者与未参加比赛的选手进行第二局的比赛,依此类推,在比赛中,有选手获胜满两局就取得比赛的胜利,比赛结束.
.比赛顺序为:首先由甲和乙进行第一局的比赛,再由获胜者与未参加比赛的选手进行第二局的比赛,依此类推,在比赛中,有选手获胜满两局就取得比赛的胜利,比赛结束.
(1)求只进行了三局比赛,比赛就结束的概率;
(2)记从比赛开始到比赛结束所需比赛的局数为ξ,求ξ的概率分布列和数学期望Eξ. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知y=f(x)是偶函数,而y=f(x+1)是奇函数,且对任意0≤x≤1,都有f(x)≥0,f(x)是增函数,则a=f(2010),b=f(
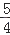 ),c=﹣f(
),c=﹣f(  )的大小关系是( )
)的大小关系是( )
A.b<c<a
B.c<b<a
C.a<c<b
D.a<b<c -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2+
 +alnx.
+alnx.(Ⅰ)若f(x)在区间[2,3]上单调递增,求实数a的取值范围;
(Ⅱ)设f(x)的导数f’(x )的图象为曲线C ,曲线C 上的不同两点A (x1, y1) ,B (x2,y 2) 所在直线的斜率为k ,求证:当a≤4时,|k|>1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
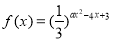 ,
,(Ⅰ)若
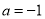 ,求
,求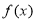 的单调区间;(Ⅱ)若
的单调区间;(Ⅱ)若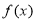 有最大值3,求
有最大值3,求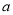 的值;(Ⅲ)若
的值;(Ⅲ)若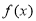 的值域是
的值域是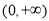 ,求
,求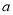 的取值范围。
的取值范围。
相关试题

