【题目】已知命题![]() 方程
方程![]() 表示焦点在
表示焦点在![]() 轴上的椭圆;命题
轴上的椭圆;命题![]() 方程
方程![]() 表示的曲线是双曲线.
表示的曲线是双曲线.
(1)若“![]() ”为真命题,求实数
”为真命题,求实数![]() 的取值范围;
的取值范围;
(2)若“![]() ”为假命题、且“
”为假命题、且“![]() ”为真命题,求实数
”为真命题,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1) ![]() 的取值范围为
的取值范围为![]() ;(2) 实数
;(2) 实数![]() 的取值范围为
的取值范围为![]() .
.
【解析】试题分析:
先求出当命题![]() 、命题
、命题![]() 分别为真命题时
分别为真命题时![]() 的取值范围.(1)由“
的取值范围.(1)由“![]() ”为真命题,可得
”为真命题,可得![]() 均为真命题,由此得到关于
均为真命题,由此得到关于![]() 的不等式组,解不等式组可得结果.(2)由“
的不等式组,解不等式组可得结果.(2)由“![]() ”为假命题、且“
”为假命题、且“![]() ”为真命题,则
”为真命题,则![]() 一真一假,分类讨论可得
一真一假,分类讨论可得![]() 的取值范围.
的取值范围.
试题解析:
(1)若![]() 为真,即方程
为真,即方程![]() 表示焦点在
表示焦点在![]() 轴上的椭圆,可得
轴上的椭圆,可得![]() ;
;
若![]() 为真,即方程
为真,即方程![]() 表示的曲线是双曲线,
表示的曲线是双曲线,
可得![]() ,
,
解得![]() 或
或![]() ;
;
∵“![]() ”为真命题,则
”为真命题,则![]() 均为真命题,
均为真命题,
∴![]() ,解得
,解得![]() .
.
∴实数![]() 的取值范围为
的取值范围为![]() ;
;
(2)若“![]() ”为假命题、且“
”为假命题、且“![]() ”为真命题,则
”为真命题,则![]() 一真一假,
一真一假,
①若![]() 真
真![]() 假,则
假,则![]() ,解得
,解得![]() ;
;
②若![]() 假
假![]() 真,则
真,则![]() ,解得
,解得![]() ,
,
综上![]() 或
或![]() .
.
∴实数![]() 的取值范围为
的取值范围为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】遂宁市观音湖港口船舶停靠的方案是先到先停.
(1)若甲乙两艘船同时到达港口,双方约定各派一名代表从1,2,3,4,5中各随机选一个数(甲、乙选取的数互不影响),若两数之和为偶数,则甲先停靠;若两数之和为奇数,则乙先停靠,这种规则是否公平?请说明理由.
(2)根据以往经验,甲船将于早上7:00~8:00到达,乙船将于早上7:30~8:30到达,请求出甲船先停靠的概率
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图三棱柱
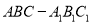 中,侧面
中,侧面 为菱形,
为菱形, 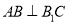 .
.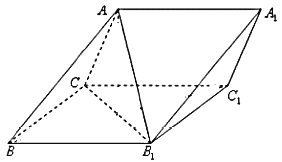
(1)证明:
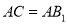 ;
;(2)若
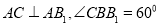 ,
, 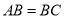 ,求二面角
,求二面角 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 :
: 的右焦点
的右焦点 ,过点
,过点 且与坐标轴不垂直的直线与椭圆交于
且与坐标轴不垂直的直线与椭圆交于 ,
, 两点,当直线
两点,当直线 经过椭圆的一个顶点时其倾斜角恰好为
经过椭圆的一个顶点时其倾斜角恰好为 .
.(1)求椭圆
 的方程;
的方程;(2)设
 为坐标原点,线段
为坐标原点,线段 上是否存在点
上是否存在点 ,使得
,使得 ?若存在,求出实数
?若存在,求出实数 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某高级中学在今年“五一”期间给校内所有教室安装了同一型号的空调,关于这批空调的使用年限
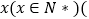 单位:年
单位:年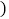 和所支出的维护费用
和所支出的维护费用 单位:千元
单位:千元 厂家提供的统计资料如表:
厂家提供的统计资料如表:x
2
4
5
6
8
y
30
40
60
50
70
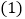 若x与y之间是线性相关关系,请求出维护费用y关于x的线性回归直线方程
若x与y之间是线性相关关系,请求出维护费用y关于x的线性回归直线方程 ;
;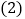 若规定当维护费用y超过
若规定当维护费用y超过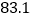 千元时,该批空调必须报度,试根据
千元时,该批空调必须报度,试根据 的结论求该批空调使用年限的最大值
的结论求该批空调使用年限的最大值 结果取整数
结果取整数 参考公式:
参考公式: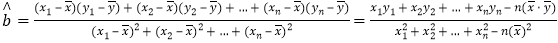 ,
,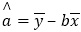 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,圆O是△ABC的外接圆,∠BAC的平分线交BC于点F,D是AF的延长线与⊙O的交点,AC的延线与⊙O的切线DE交于点E.
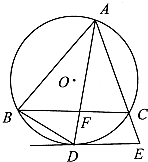
(1)求证: =
= 
(2)若BD=3 ,EC=2,CA=6,求BF的值.
,EC=2,CA=6,求BF的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某体校为了备战明年四月份省划艇单人双桨比赛,对本校甲、乙两名划艇运动员在相同条件下进行了6次测试,测得他们划艇最大速度
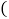 单位:
单位: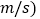 数据如下:
数据如下:甲:27,38,30,37,35,31;
乙:33,29,38,34,28,36.
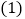 试用茎叶图表示甲、乙两名运动员测试的成绩;
试用茎叶图表示甲、乙两名运动员测试的成绩;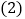 根据测试的成绩,你认为派哪名运动员参加明年四月份的省划艇单人双桨比赛比较合适?并说明你的理由
根据测试的成绩,你认为派哪名运动员参加明年四月份的省划艇单人双桨比赛比较合适?并说明你的理由
相关试题

