【题目】为了解某单位员工的月工资水平,从该单位500位员工中随机抽取了50位进行调查,得到如下频数分布表和频率分布直方图:
月工资 (单位:百元) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
男员工数 | 1 | 8 | 10 | 6 | 4 | 4 |
女员工数 | 4 | 2 | 5 | 4 | 1 | 1 |
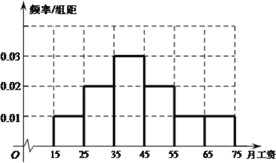
(1)![]() 试由上图估计该单位员工月平均工资;
试由上图估计该单位员工月平均工资;
(2)现用分层抽样的方法从月工资在![]() 和
和![]() 的两组所调查的男员工中随机选取5人,问各应抽取多少人?
的两组所调查的男员工中随机选取5人,问各应抽取多少人?
(3)若从月工资在![]() 和
和![]() 两组所调查的女员工中随机选取2人,试求这2人月工资差不超过1000元的概率.
两组所调查的女员工中随机选取2人,试求这2人月工资差不超过1000元的概率.
参考答案:
【答案】(1) 估计为4300元;(2) 分别抽取3人,2人;(3) ![]() .
.
【解析】试题分析:(1)平均值等于各个小矩形的面积乘以组中值之和;(2)易得两层的人数比为![]() ,故分别为
,故分别为![]() 人,
人,![]() 人;(3) 由已知可得从
人;(3) 由已知可得从![]() 人选
人选![]() 人有
人有![]() 种,古河条件的有
种,古河条件的有![]() 种,故所求概率为
种,故所求概率为![]() .
.
试题解析:
(1) ![]()
即该单位员工月平均工资估计为4300元.
(2)分别抽取3人,2人
(3)由上表可知:月工资在![]() 组的有两名女工,分别记作甲和乙;月工资在
组的有两名女工,分别记作甲和乙;月工资在![]() 组的有四名女工,分别记作A,B,C,D.现在从这6人中随机选取2人的基本事件有如下15组:
组的有四名女工,分别记作A,B,C,D.现在从这6人中随机选取2人的基本事件有如下15组:
(甲,乙),(甲,A),(甲,B),(甲,C),(甲,D),
(乙,A),(乙,B),(乙,C),(乙,D),
(A,B),(A,C),(A,D),
(B,C),(B,D),
(C,D)
其中月工资差不超过1000元,即为同一组的有(甲,乙),(A,B),(A,C),(A,D),(B,C),(B,D),(C,D)共7组,
∴所求概率为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年12月16日,科幻片《侠盗一号》上映,上映至今,全球累计票房高达8亿美金.为了了解娄底观众的满意度,某影院随机调查了本市观看影片的观众,并用“10分制”对满意度进行评分,分数越高满意度越高,若分数不低于9分,则称该观众为“满意观众”.现从调查人群中随机抽取12名.如图所示的茎叶图记录了他们的满意度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶).
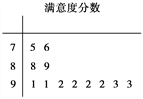
(1)求从这12人中随机选取1人,该人不是“满意观众”的概率;
(2)从本次所记录的满意度评分大于9.1的“满意观众”中随机抽取2人,求这2人得分不同的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了参加师大附中第30届田径运动会的开幕式,高三年级某6个班联合到集市购买了6根竹竿,作为班期的旗杆之用,它们的长度分别为3.8,4.3,3.6,4.5,4.0,4.1(单位:米).
(1)若从中随机抽取两根竹竿,求长度之差不超过0.5米的概率;
(2)若长度不小于4米的竹竿价格为每根10元,长度小于4米的竹竿价格为每根
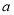 元.从这6根竹竿中随机抽取两根,若期望这两根竹竿的价格之和为18元,求
元.从这6根竹竿中随机抽取两根,若期望这两根竹竿的价格之和为18元,求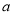 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
 中,以
中,以 为极点,
为极点,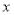 轴的非负半轴为极轴建立的极坐标系中,直线
轴的非负半轴为极轴建立的极坐标系中,直线 的极坐标方程为
的极坐标方程为 (
(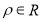 ),曲线
),曲线 的参数方程为
的参数方程为
(1)写出直线
 及曲线
及曲线 的直角坐标方程;
的直角坐标方程;(2)过点
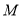 平行于直线
平行于直线 的直线与曲线
的直线与曲线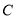 交于
交于 、
、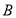 两点,若
两点,若 ,求点
,求点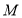 轨迹的直角坐标方程.
轨迹的直角坐标方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
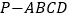 中,底面
中,底面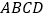 为平行四边形,
为平行四边形, 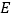 为侧棱
为侧棱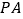 的中点.
的中点.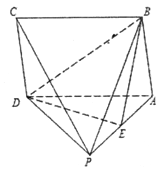
(Ⅰ)求证:
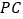 ∥平面
∥平面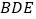
(Ⅱ)若
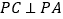 ,
,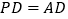 ,
,求证:平面
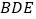
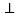 平面
平面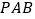
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,棱形
 的边长为6,
的边长为6, 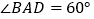 ,
,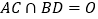 .将棱形
.将棱形 沿对角线
沿对角线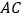 折起,得到三棱锥
折起,得到三棱锥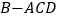 ,点
,点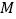 是棱
是棱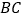 的中点,
的中点, 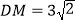 .
.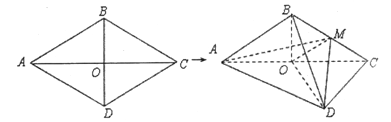
(Ⅰ)求证:
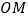 ∥平面
∥平面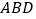 ;
;(Ⅱ)求三棱锥
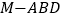 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】“奶茶妹妹”对某时间段的奶茶销售量及其价格进行调查,统计出售价
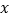 元和销售量
元和销售量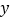 杯之间的一组数据如下表所示:
杯之间的一组数据如下表所示:价格
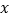
5
5.5
6.5
7
销售量
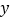
12
10
6
4
通过分析,发现销售量
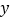 对奶茶的价格
对奶茶的价格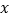 具有线性相关关系.
具有线性相关关系.(Ⅰ)求销售量
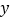 对奶茶的价格
对奶茶的价格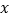 的回归直线方程;
的回归直线方程;(Ⅱ)欲使销售量为
 杯,则价格应定为多少?
杯,则价格应定为多少?附:线性回归方程为
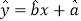 ,其中
,其中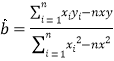 ,
,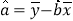
相关试题

