【题目】如图,在正方体![]() 中,
中,![]() ,
,![]() 分别是棱
分别是棱![]() ,
,![]() 的中点,
的中点,![]() 为棱
为棱![]() 上一点,
上一点,![]() 且
且![]() 平面
平面![]() .
.

(1)证明:![]() 为
为![]() 中点;
中点;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
参考答案:
【答案】(1)见解析;(2)锐二面角的余弦值为![]() .
.
【解析】试题分析:(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,利用
,利用![]() ,
,![]() 证得四边形
证得四边形![]() 为平行四边形,则
为平行四边形,则![]() ,所以
,所以![]() 为
为![]() 的中点;
的中点;
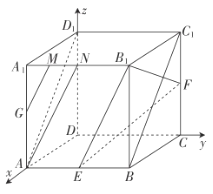
(2)以![]() 为坐标原点,建立如图所示的空间直角坐标系
为坐标原点,建立如图所示的空间直角坐标系![]() .不妨令正方体的棱长为2,利用两个面的法向量求解即可.
.不妨令正方体的棱长为2,利用两个面的法向量求解即可.
试题解析:
(1)证明:取![]() 的中点
的中点![]() ,连接
,连接![]() ,因为
,因为![]() ,所以
,所以![]() 为
为![]() 的中点,又
的中点,又![]() 为
为![]() 的中点,所以
的中点,所以![]() ,因为
,因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,所以
,所以![]() ,即
,即![]() ,又
,又![]() ,所以四边形
,所以四边形![]() 为平行四边形,则
为平行四边形,则![]() ,所以
,所以![]() 为
为![]() 的中点.
的中点.
(2)解:以![]() 为坐标原点,建立如图所示的空间直角坐标系
为坐标原点,建立如图所示的空间直角坐标系![]() .不妨令正方体的棱长为2,则
.不妨令正方体的棱长为2,则![]() ,可得
,可得![]() ,
,![]() ,设
,设![]() 是平面
是平面![]() 的法向量,则
的法向量,则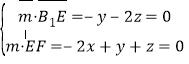 .令
.令![]() ,得
,得![]() .
.
易得平面![]() 的一个法向量为
的一个法向量为![]() ,
,
所以![]()
![]() .
.
故所求锐二面角的余弦值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 过点
过点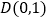 ,且离心率为
,且离心率为 .过抛物线
.过抛物线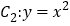 上一点
上一点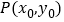 作
作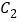 的切线
的切线 交椭圆
交椭圆 于
于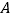 ,
,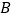 两点.
两点.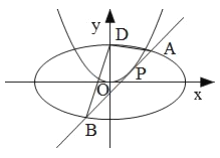
(Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)是否存在直线
 ,使得
,使得 ,若存在,求出
,若存在,求出 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在人群流量较大的街道,有一中年人吆喝“送钱”,只见他手拿一黑色小布袋,袋中有3只黄色、3只白色的乒乓球(其体积、质地完成相同),旁边立着一块小黑板写道:
摸球方法:从袋中随机摸出3个球,若摸得同一颜色的3个球,摊主送给摸球者5元钱;若摸得非同一颜色的3个球,摸球者付给摊主1元钱.
(1)摸出的3个球为白球的概率是多少?
(2)摸出的3个球为2个黄球1个白球的概率是多少?
(3)假定一天中有100人次摸奖,试从概率的角度估算一下这个摊主一个月(按30天计)能赚多少钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(Ⅰ)求函数
 的单调区间;
的单调区间;(Ⅱ)若
 ,求证:
,求证: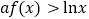 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某良种培育基地正在培育一种小麦新品种A,将其与原有的一个优良品种B进行对照试验,两种小麦各种植了24亩,所得亩产数据(单位:千克)如下:
品种A:357,359,367,368,375,388,392,399,400,405,412,414,415,421,423,423,427,430,430,434,443,445,451,454
品种B:363,371,374,383,385,386,391,392,394,395,397,397,400,401,401,403,406,407,410,412,415,416,422,430
(1)画出茎叶图.
(2)用茎叶图处理现有的数据,有什么优点?
(3)通过观察茎叶图,对品种A与B的亩产量及其稳定性进行比较,写出统计结论。
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛. 为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计. 请你根据尚未完成并有局部污损的频率分布表和频数分布直方图,解答下列问题:


(1)填充频率分布表的空格(将答案直接填在表格内);
(2)补全频数分布直方图;
(3)若成绩在75.585.5分的学生为二等奖,问获得二等奖的学生约为多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
 中,直线
中,直线 的参数方程为
的参数方程为 (
( 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,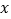 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线 的极坐标方程为
的极坐标方程为 .
.(1)写出直线
 的普通方程及曲线
的普通方程及曲线 的直角坐标方程;
的直角坐标方程;(2)已知点
 ,点
,点 ,直线
,直线 过点
过点 且与曲线
且与曲线 相交于
相交于 ,
, 两点,设线段
两点,设线段 的中点为
的中点为 ,求
,求 的值.
的值.
相关试题

