【题目】已知函数f(x)=﹣2sin(2x+φ)(|φ|<π),若 ![]() ,则f(x)的一个单调递增区间可以是( )
,则f(x)的一个单调递增区间可以是( )
A.![]()
B.![]()
C.![]()
D.![]()
参考答案:
【答案】D
【解析】解:∵当x= ![]() 时,f(x)=﹣2sin(2x+φ)有最小值为﹣2
时,f(x)=﹣2sin(2x+φ)有最小值为﹣2
∴x= ![]() 是方程2x+φ=
是方程2x+φ= ![]() +2kπ的一个解,得φ=
+2kπ的一个解,得φ= ![]() +2kπ,(k∈Z)
+2kπ,(k∈Z)
∵|φ|<π,∴取k=0,得φ= ![]() .
.
因此函数表达式为:f(x)=﹣2sin(2x+ ![]() )
)
令 ![]() +2kπ≤2x+
+2kπ≤2x+ ![]() ≤
≤ ![]() +2kπ,得
+2kπ,得 ![]() +kπ≤x≤
+kπ≤x≤ ![]() +kπ,(k∈Z)
+kπ,(k∈Z)
取k=0,得f(x)的一个单调递增区间是 ![]()
故选:D
【考点精析】根据题目的已知条件,利用正弦函数的单调性的相关知识可以得到问题的答案,需要掌握正弦函数的单调性:在![]()
![]() 上是增函数;在
上是增函数;在![]()
![]() 上是减函数.
上是减函数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】1979年,李政道博士给中国科技大学少年班出过一道智趣题:5只猴子分一堆桃子,怎么也不能分成5等份,只好先去睡觉,准备第二天再分,夜里1只猴子偷偷爬起来,先吃掉一个桃子,然后将其分成5等份,藏起自己的一份就去睡觉了;第2只猴子又爬起来,将剩余的桃子吃掉一个后,也将桃子分成5等份;藏起自己的一份睡觉去了;以后的3只猴子都先后照此办理,问:最初至少有多少个桃子?最后至少剩下多少个桃子?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱柱
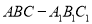 中,四边形
中,四边形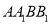 是菱形,
是菱形,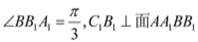 ,二面角
,二面角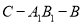 为
为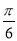 ,
,  .
.(Ⅰ)求证:平面
 平面
平面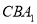 ;
;(Ⅱ)求二面角
 的余弦值.
的余弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)是定义在R上的偶函数,当x≥0时,f(x)=x2﹣2x﹣1.
(1)求f(x)的函数解析式,并用分段函数的形式给出;
(2)作出函数f(x)的简图;
(3)写出函数f(x)的单调区间及最值. -
科目: 来源: 题型:
查看答案和解析>>【题目】为得到函数y=sin(2x+
 )的图象,只需将函数y=sin2x的图象( )
)的图象,只需将函数y=sin2x的图象( )
A.向右平移 长度单位
长度单位
B.向左平移 个长度单位
个长度单位
C.向右平移个 长度单位
长度单位
D.向左平移 长度单位
长度单位 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,圆C:x2+y2﹣8y+12=0,直线l:ax+y+2a=0.
(1)当a为何值时,直线l与圆C相切;
(2)当直线l与圆C相交于A、B两点,且AB=2 时,求直线l的方程.
时,求直线l的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】随着社会发展,淮北市在一天的上下班时段也出现了堵车严重的现象。交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念.记交通指数为T,其范围为[0,10],分别有5个级别:T∈[0,2)畅通;T∈[2,4)基本畅通;T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.早高峰时段(T≥3 ),从淮北市交通指挥中心随机选取了一至四马路之间50个交通路段,依据交通指数数据绘制的直方图如图所示:
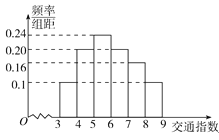
(I)据此直方图估算交通指数T∈[4,8)时的中位数和平均数;
(II)据此直方图求出早高峰一至四马路之间的3个路段至少有2个严重拥堵的概率是多少?
(III)某人上班路上所用时间若畅通时为20分钟,基本畅通为30分钟,轻度拥堵为35分钟,中度拥堵为45分钟,严重拥堵为60分钟,求此人用时间的数学期望.
相关试题

