【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,S表示△ABC的面积,若acosB+bcosA=csinC,S= ![]() (b2+c2﹣a2),则∠B=( )
(b2+c2﹣a2),则∠B=( )
A.90°
B.60°
C.45°
D.30°
参考答案:
【答案】C
【解析】解:由正弦定理可知acosB+bcosA=2RsinAcosB+2RsinBcosA=2Rsin(A+B)=2RsinC=2RsinCsinC
∴sinC=1,C= ![]() .
.
∴S= ![]() ab=
ab= ![]() (b2+c2﹣a2),
(b2+c2﹣a2),
解得a=b,因此∠B=45°.
故选C
先利用正弦定理把题设等式中的边转化成角的正弦,化简整理求得sinC的值,进而求得C,然后利用三角形面积公式求得S的表达式,进而求得a=b,推断出三角形为等腰直角三角形,进而求得∠B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,内角A,B,C成等差数列,其对边a,b,c满足2b2=3ac,求A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设命题p:函数y=sin2x的最小正周期为
 ;命题q:函数y=cosx的图象关于直线x=
;命题q:函数y=cosx的图象关于直线x=  对称.则下列判断正确的是( )
对称.则下列判断正确的是( )
A.p为真
B.¬q为假
C.p∧q为假
D.p∨q为真 -
科目: 来源: 题型:
查看答案和解析>>【题目】设z1 , z2是复数,则下列命题中的假命题是( )
A.若|z1﹣z2|=0,则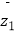 =
= 
B.若z1= ,则
,则 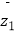 =z2
=z2
C.若|z1|=|z2|,则z1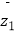 =z2
=z2 
D.若|z1|=|z2|,则z12=z22 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,正方体ABCD﹣A1B1C1D1的棱长为a,M,N分别为A1B和AC上的点,A1M=AN=
 ,则MN与平面BB1C1C的位置关系为( )
,则MN与平面BB1C1C的位置关系为( ) 
A.相交
B.平行
C.垂直
D.不能确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】某地西红柿从
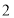 月
月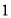 日起开始上市.通过市场调查,得到西红柿种植成本
日起开始上市.通过市场调查,得到西红柿种植成本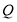 (就是每
(就是每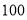 公斤西红柿的种植成本,单位:元)与上市时间
公斤西红柿的种植成本,单位:元)与上市时间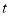 (单位:天)的数据如下表:
(单位:天)的数据如下表:上市时间
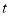
50
110
250
种植成本
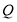
150
108
150
(1)根据上表数据,从下列函数中选取一个函数描述西红柿种植成本与上市时间
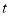 的变化关系:
的变化关系: ;
; ;
;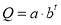 ;
;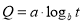 ,并求出函数解析式;
,并求出函数解析式;(2)利用你选取的函数,求西红柿种植成本最低时的上市天数及最低种植成本.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图C,D是以AB为直径的圆上的两点,
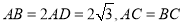 ,F是AB上的一点,且
,F是AB上的一点,且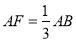 ,将圆沿AB折起,使点C在平面ABD的射影E在BD上,已知
,将圆沿AB折起,使点C在平面ABD的射影E在BD上,已知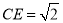

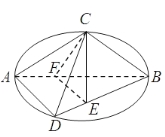
(1)求证:AD
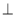 平面BCE
平面BCE(2)求证:AD//平面CEF;
(3)求三棱锥A-CFD的体积.
相关试题

