【题目】已知公比不为1的等比数列{an}的前3项积为27,且2a2为3a1和a3的等差中项.
(1)求数列{an}的通项公式an;
(2)若数列{bn}满足bn=bn﹣1log3an+1(n≥2,n∈N*),且b1=1,求数列{ ![]() }的前n项和Sn .
}的前n项和Sn .
参考答案:
【答案】
(1)解:设{an}的公比为q,
则a1a2a3=a23=27,∴a2=3,∴a1= ![]() ,a3=3q,
,a3=3q,
∵2a2为3a1和a3的等差中项,
∴4a2=3a1+a3,即12= ![]() +3q,解得q=3或q=1(舍).
+3q,解得q=3或q=1(舍).
∴an=3n﹣1.
(2)解:∵bn=bn﹣1log3an+1=nbn﹣1,
∴ ![]() =n,又b1=1,
=n,又b1=1,
∴bn= ![]()
![]()
![]() …
… ![]() =n!,
=n!,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() ﹣
﹣ ![]() ,
,
∴Sn=( ![]() ﹣
﹣ ![]() )+(
)+( ![]() ﹣
﹣ ![]() )+…+(
)+…+( ![]() ﹣
﹣ ![]() )=
)= ![]() ﹣
﹣ ![]() =
= ![]() .
.
【解析】(1)利用等比数列的性质列方程解出公比和a2 , 从而得出通项an;(2)化简递推式可得 ![]() =n,使用累乘法得出通项bn , 从而得出{
=n,使用累乘法得出通项bn , 从而得出{ ![]() }的通项,利用裂项法求出Sn .
}的通项,利用裂项法求出Sn .
【考点精析】本题主要考查了数列的前n项和的相关知识点,需要掌握数列{an}的前n项和sn与通项an的关系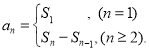 才能正确解答此题.
才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知三角形的顶点为A(2,4),B(0,-2),C(-2,3),求:
(1)直线AB的方程;
(2)AB边上的高所在直线的方程;
(3)AB的中位线所在的直线方程.

-
科目: 来源: 题型:
查看答案和解析>>【题目】先后抛掷两枚骰子,设出现的点数之和是12,11,10的概率依次是P1,P2,P3,则( )
(A)P1=P2<P3 (B)P1<P2<P3 (C)P1<P2=P3 (D)P3=P2<P1
-
科目: 来源: 题型:
查看答案和解析>>【题目】街道旁边有一游戏:在铺满边长为9 cm的正方形塑料板的宽广地面上,掷一枚半径为1 cm的小圆板,规则如下:每掷一次交5角钱,若小圆板压在正方形的边上,可重掷一次;若掷在正方形内,须再交5角钱可玩一次;若掷在或压在塑料板的顶点上,可获得一元钱,试问:
(1)小圆板压在塑料板的边上的概率是多少?
(2)小圆板压在塑料板顶点上的概率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在5件产品中,有3件一等品和2件二等品,从中任取2件,以
 为概率的事件是( )
为概率的事件是( )A. 恰有1件一等品 B. 至少有一件一等品
C. 至多有一件一等品 D. 都不是一等品
-
科目: 来源: 题型:
查看答案和解析>>【题目】华中师大附中中科教处为了研究高一学生对物理和数学的学习是否与性别有关,从高一年级抽取60名同学(男同学30名,女同学30名),给所有同学物理题和数学题各一题,让每位同学自由选择一道题进行解答.选题情况如表:(单位:人)
物理题
数学题
总计
男同学
16
14
30
女同学
8
22
20
总计
24
36
60
(1)在犯错误的概率不超过1%的条件下,能否判断高一学生对物理和数学的学习与性别有关?
(2)经过多次测试后发现,甲每次解答一道物理题所用的时间为5﹣8分钟,乙每次解答一道物理题所用的时间为6﹣8分钟,现甲、乙解同一道物理题,求甲比乙先解答完的概率;
(3)现从选择做物理题的8名女生中任意选取两人,对他们的解答情况进行全程研究,记甲、乙两女生被抽到的人数为X,求X的分布列和数学期望. 附表及公式:P(K2k)
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k
2.072
2.706
3.841
5.024
6.635
7.879
10.828
K2=
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】传承传统文化再掀热潮,我校举行传统文化知识竞赛.其中两位选手在个人追逐赛中的比赛得分如茎叶图所示,则下列说法正确的是( )

A. 甲的平均数大于乙的平均数
B. 甲的中位数大于乙的中位数
C. 甲的方差大于乙的方差
D. 甲的平均数等于乙的中位数
相关试题

