【题目】若某一等差数列的首项为![]() ,公差为
,公差为![]() 展开式中的常数项,其中
展开式中的常数项,其中![]() 是
是![]() 除以19的余数,则此数列前多少项的和最大?并求出这个最大值.
除以19的余数,则此数列前多少项的和最大?并求出这个最大值.
参考答案:
【答案】此数列的前25项之和与前26项之和相等且最大,![]() .
.
【解析】
根据题意,由排列、组合数的性质,可得不等式![]() ,解可得n的范围,结合n∈N,可得n的值,进而可得首项a1,对7777﹣15变形,结合二项式定理可得m的值,从而可得数列的公差,即可得数列的通项公式,根据等差数列的性质,设其前k项之和最大,则
,解可得n的范围,结合n∈N,可得n的值,进而可得首项a1,对7777﹣15变形,结合二项式定理可得m的值,从而可得数列的公差,即可得数列的通项公式,根据等差数列的性质,设其前k项之和最大,则![]() ,解可得k=25或k=26,可得答案.
,解可得k=25或k=26,可得答案.
由已知得:![]() ,又
,又![]() ,
,
![]()
![]() 故
故![]() .
.
![]()
![]()
![]() ,所以
,所以![]() 除以19的余数是5,即
除以19的余数是5,即![]()
![]() 的展开式的通项
的展开式的通项![]()
![]() ,若它为常数项,则
,若它为常数项,则![]() ,代入上式
,代入上式![]() .从而等差数列的通项公式是:
.从而等差数列的通项公式是:![]() ,……10分
,……10分
设其前k项之和最大,则![]() ,解得k=25或k=26,
,解得k=25或k=26,
故此数列的前25项之和与前26项之和相等且最大,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从6名短跑运动员中选出4人参加4×100 m接力赛.试求满足下列条件的参赛方案各有多少种?(用数字作答)
(1)甲不能跑第一棒和第四棒;(2)甲不能跑第一棒,乙不能跑第四棒
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知平面ADC∥平面A1B1C1 , B为线段AD的中点,△ABC≈△A1B1C1 , 四边形ABB1A1为正方形,平面AA1C1C丄平面ADB1A1 , A1C1=A1A,∠C1A1A=
 ,M为棱A1C1的中点.
,M为棱A1C1的中点.
(Ⅰ)若N为线段DC1上的点,且直线MN∥平面ADB1A1 , 试确定点N的位置;
(Ⅱ)求平面MAD与平面CC1D所成的锐二面角的余弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设A={x|2x2+ax+2=0},B={x|x2+3x+2a=0},且A∩B={2}.
(1)求a的值及集合A,B;
(2)设全集U=A∪B,求(UA)∪(UB);
-
科目: 来源: 题型:
查看答案和解析>>【题目】某闯关游戏规则是:先后掷两枚骰子,将此试验重复n轮,第n轮的点数分别记为xn , yn , 如果点数满足xn<
 ,则认为第n轮闯关成功,否则进行下一轮投掷,直到闯关成功,游戏结束.
,则认为第n轮闯关成功,否则进行下一轮投掷,直到闯关成功,游戏结束.
(Ⅰ)求第一轮闯关成功的概率;
(Ⅱ)如果第i轮闯关成功所获的奖金数f(i)=10000× (单位:元),求某人闯关获得奖金不超过1250元的概率;
(单位:元),求某人闯关获得奖金不超过1250元的概率;
(Ⅲ)如果游戏只进行到第四轮,第四轮后不论游戏成功与否,都终止游戏,记进行的轮数为随机变量X,求x的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
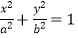 (a>b>0)的短轴长为2,过上顶点E和右焦点F的直线与圆M:x2+y2﹣4x﹣2y+4=0相切.
(a>b>0)的短轴长为2,过上顶点E和右焦点F的直线与圆M:x2+y2﹣4x﹣2y+4=0相切.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若直线l过点(1,0),且与椭圆C交于点A,B,则在x轴上是否存在一点T(t,0)(t≠0),使得不论直线l的斜率如何变化,总有∠OTA=∠OTB (其中O为坐标原点),若存在,求出 t的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 (a,b∈R,且a≠0,e为自然对数的底数).
(a,b∈R,且a≠0,e为自然对数的底数).
(1)若曲线f(x)在点(e,f(e))处的切线斜率为0,且f(x)有极小值,求实数a的取值范围.
(2)①当 a=b=l 时,证明:xf(x)+2<0; ②当 a=1,b=﹣1 时,若不等式:xf(x)>e+m(x﹣1)在区间(1,+∞)内恒成立,求实数m的最大值.
相关试题

