【题目】已知数列![]() 满足
满足![]() ,
, ![]() ,其中
,其中![]() .
.
(1)设![]() ,求证:数列
,求证:数列![]() 是等差数列,并求出
是等差数列,并求出![]() 的通项公式;
的通项公式;
(2)设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,是否存在正整数
,是否存在正整数![]() ,使得
,使得![]() 对于
对于![]() 恒成立,若存在,求出
恒成立,若存在,求出![]() 的最小值,若不存在,请说明理由.
的最小值,若不存在,请说明理由.
参考答案:
【答案】(1) ![]() ;(2)
;(2) ![]() 的最小值为3.
的最小值为3.
【解析】试题分析:(1)利用递推公式即可得出![]() 为一个常数,从而证明数列
为一个常数,从而证明数列![]() 是等差数,再利用等差数列的通项公式即可得到
是等差数,再利用等差数列的通项公式即可得到![]() ,进而得到
,进而得到![]() ;(2)利用(1)的结论,利用“裂项求和”即可得到
;(2)利用(1)的结论,利用“裂项求和”即可得到![]() ,要使得
,要使得![]() 对于
对于![]() 恒成立,只要
恒成立,只要![]() ,即
,即![]() ,解出即可.
,解出即可.
试题解析:(1)证明: 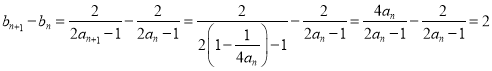 ,
,
所以数列![]() 是等差数列,
是等差数列,
![]() ,因此
,因此![]() ,
,
由![]() .
.
(2)由![]() ,
,
所以![]() ,
,
所以![]() ,
,
因为![]() ,所以
,所以![]() 恒成立,
恒成立,
依题意要使![]() 对于
对于![]() ,恒成立,只需
,恒成立,只需![]() ,且
,且![]() 解得
解得![]() ,
, ![]() 的最小值为
的最小值为![]() .
.
【方法点晴】裂项相消法是最难把握的求和方法之一,其原因是有时很难找到裂项的方向,突破这一难点的方法是根据式子的结构特点,掌握一些常见的裂项技巧:①![]() ;②
;②![]()
![]() ;③
;③![]() ;
;
④![]()
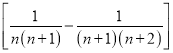 ;此外,需注意裂项之后相消的过程中容易出现丢项或多项的问题,导致计算结果错误.
;此外,需注意裂项之后相消的过程中容易出现丢项或多项的问题,导致计算结果错误.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
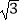 sin(2x+
sin(2x+  ),其中x∈R,下列结论中正确的是( )
),其中x∈R,下列结论中正确的是( )
A.f(x)是最小正周期为π的偶函数
B.f(x)的一条对称轴是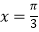
C.f(x)的最大值为2
D.将函数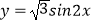 的图象向左平移
的图象向左平移  个单位得到函数f(x)的图象
个单位得到函数f(x)的图象 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<
 )的最小正周期是π,若其图象向右平移
)的最小正周期是π,若其图象向右平移  个单位后得到的函数为奇函数,则函数y=f(x)的图象( )
个单位后得到的函数为奇函数,则函数y=f(x)的图象( )
A.关于点( ,0)对称
,0)对称
B.关于直线x= 对称
对称
C.关于点(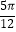 ,0)对称
,0)对称
D.关于直线x=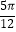 对称
对称 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图的茎叶图是甲、乙两人在4次模拟测试中的成绩,其中一个数字被污损,则甲的平均成绩不超过乙的平均成绩的概率为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】动点
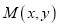 分别到两定点
分别到两定点
 连线的斜率之乘积为
连线的斜率之乘积为 ,设
,设 的轨迹为曲线
的轨迹为曲线 ,
,  ,
,  分别为曲线
分别为曲线 的左右焦点,则下列命题中:
的左右焦点,则下列命题中:(1)曲线
 的焦点坐标为
的焦点坐标为 ,
, 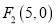 ;
;(2)若
 ,则
,则
 ;
;(3)当
 时,
时,  的内切圆圆心在直线
的内切圆圆心在直线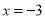 上;
上;(4)设
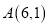 ,则
,则 的最小值为
的最小值为 .
.其中正确命题的序号是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
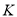 :
: 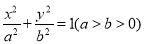 的左、右焦点分别为
的左、右焦点分别为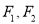 ,其离心率
,其离心率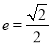 ,以原点为圆心,椭圆的半焦距为半径的圆与直线
,以原点为圆心,椭圆的半焦距为半径的圆与直线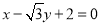 相切.
相切.(1)求
 的方程;
的方程;(2)过
 的直线
的直线 交
交 于
于 两点,
两点, 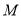 为
为 的中点,连接
的中点,连接 并延长交
并延长交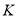 于点
于点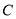 ,若四边形
,若四边形 的面积
的面积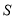 满足:
满足:  ,求直线
,求直线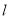 的斜率.
的斜率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
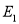 :
: 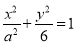 的焦点
的焦点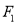 、
、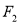 在
在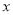 轴上,且椭圆
轴上,且椭圆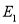 经过
经过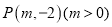 ,过点
,过点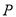 的直线
的直线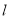 与
与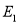 交于点
交于点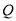 ,与抛物线
,与抛物线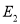 :
: 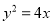 交于
交于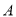 、
、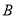 两点,当直线
两点,当直线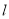 过
过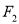 时
时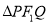 的周长为
的周长为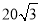 .
.(Ⅰ)求
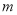 的值和
的值和 的方程;
的方程;(Ⅱ)以线段
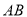 为直径的圆是否经过
为直径的圆是否经过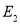 上一定点,若经过一定点求出定点坐标,否则说明理由。
上一定点,若经过一定点求出定点坐标,否则说明理由。
相关试题

