【题目】设函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)当![]() 时,
时, ![]() ,求
,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)见解析(2)![]() .
.
【解析】试题分析:(1)根据![]() ,对字母a分类讨论,求出函数的单调区间;(2)当
,对字母a分类讨论,求出函数的单调区间;(2)当![]() 时,分离参数,转化为分别求
时,分离参数,转化为分别求![]() 的最小值,及
的最小值,及![]() 的最大值,利用导数,求其
的最大值,利用导数,求其![]() 最大值即可.
最大值即可.
试题解析:(1)![]() .
.
若![]() ,则
,则![]() ,在
,在![]() 单调递增.若
单调递增.若![]() ,当
,当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .于是
.于是![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
(2)方法1:当![]() 时,
时, ![]() ,即
,即![]()
因为函数![]() 在
在![]() 单调递增,所以
单调递增,所以![]() .
.
设![]() ,
, ![]() ,当
,当![]() 时,
时, ![]() ,
, ![]() 单调递增;当
单调递增;当![]() 时,
时, ![]() ,
, ![]() 单调递减.故
单调递减.故![]()
![]() ,所以
,所以![]() .综上,
.综上, ![]() 的取值范围为
的取值范围为![]() .
.
(2)方法2:设![]() ,则当
,则当![]() 时,
时, ![]() .
.
由![]() ,得
,得![]() .
.
![]() ,当
,当![]() 时,
时, ![]() ,
, ![]() 单调递增,所以
单调递增,所以![]() .
.
若![]() ,当
,当![]() 时,
时, ![]() ,
, ![]() 单调递增,故
单调递增,故![]() .因为
.因为![]() ,所以
,所以![]() .
.
若![]() ,由
,由![]() ,
, ![]() ,知
,知![]() 在
在![]() 存在唯一零点,设为
存在唯一零点,设为![]() ,则
,则![]() .
.
当![]() 时,
时, ![]() ,
, ![]() 单调递减;当
单调递减;当![]() 时,
时, ![]() ,
, ![]() 单调递增;故
单调递增;故![]() 在
在![]() 有最小值
有最小值![]() ,而
,而![]() .由
.由![]() 得
得![]() .
.
由(1)得![]() 在
在![]() 单调递减,所以
单调递减,所以![]() .
.
综上, ![]() 的取值范围为
的取值范围为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
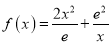 ,
, 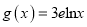 ,其中
,其中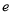 为自然对数的底数.
为自然对数的底数.(Ⅰ)讨论函数
 的单调性.
的单调性.(Ⅱ)试判断曲线
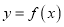 与
与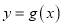 是否存在公共点并且在公共点处有公切线.若存在,求出公切线
是否存在公共点并且在公共点处有公切线.若存在,求出公切线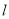 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两家外卖公司,其送餐员的日工资方案如下:甲公司的底薪70元,每单抽成3元;乙公司无底薪,40单以内(含40单)的部分每单抽成5元,超出40单的部分每单抽成7元,假设同一公司送餐员一天的送餐单数相同,现从两家公司各随机抽取一名送餐员,并分别记录其100天的送餐单数,得到频数表如下:
甲公司送餐员送餐单数频数表
送餐单数
38
39
40
41
42
天数
20
40
20
10
10
乙公司送餐员送餐单数频数表
送餐单数
38
39
40
41
42
天数
10
20
20
40
10
将上表中的频率视为概率,回答下列问题:
(1)现从甲公司随机抽取3名送餐员,求恰有2名送餐员送餐单数超过40的概率;
(2)(i)记乙公司送餐员日工资为X(单位:元),求X的数学期望;
(ii)某人拟到甲、乙两家公司中的一家应聘送餐员,如果仅从日平均工资的角度考虑,他应该选择去哪家公司应聘,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】长方形
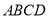 中,
中, 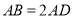 ,
, 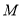 是
是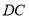 中点(图1).将△
中点(图1).将△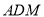 沿
沿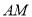 折起,使得
折起,使得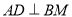 (图2)在图2中:
(图2)在图2中: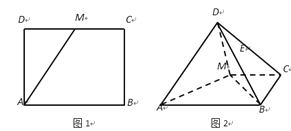
(1)求证:平面
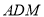
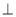 平面
平面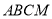 ;
; (2)在线段
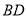 上是否存点
上是否存点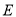 ,使得二面角
,使得二面角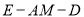 为大小为
为大小为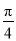 ,说明理由.
,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知不等式|y+4|-|y|≤2x+
 对任意实数x,y都成立,则常数a的最小值为( )
对任意实数x,y都成立,则常数a的最小值为( )A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知m,n∈R+,f(x)=|x+m|+|2x-n|.
(1)当m=n=1时,求f(x)的最小值;
(2)若f(x)的最小值为2,求证
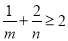 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知正项等比数列{an}(n∈N*),首项a1=3,前n项和为Sn,且S3+a3、S5+a5,S4+a4成等差数列.
(1)求数列{an}的通项公式;
(2)数列{nan}的前n项和为Tn,若对任意正整数n,都有Tn∈[a,b],求b-a的最小值.
相关试题

