【题目】已知椭圆![]() ,与
,与![]() 轴的正半轴交于点
轴的正半轴交于点![]() ,右焦点
,右焦点![]() ,
, ![]() 为坐标原点,且
为坐标原点,且![]() .
.
(1)求椭圆的离心率![]() ;
;
(2)已知点![]() ,过点
,过点![]() 任意作直线
任意作直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,设直线
两点,设直线![]() 的斜率
的斜率![]() ,若
,若![]() ,求椭圆
,求椭圆![]() 的方程.
的方程.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)tan∠PFO=![]() 可得
可得![]() =
=![]() ,c=
,c=![]() b,a=
b,a=![]() =
=![]() b即可得出(2)直线斜率不为0时,设出直线方程ty=x﹣1,设C(x1,y1),D(x2,y2).联立
b即可得出(2)直线斜率不为0时,设出直线方程ty=x﹣1,设C(x1,y1),D(x2,y2).联立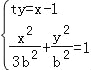 ,化为:(t2+3)y2+2ty+1﹣3b2=0,∵k1+k2=2,∴
,化为:(t2+3)y2+2ty+1﹣3b2=0,∵k1+k2=2,∴![]() +
+![]() =2,根据韦达定理代入求解即可,斜率为0 时也成立
=2,根据韦达定理代入求解即可,斜率为0 时也成立
试题解析:
(1)∵tan∠PFO=![]() ,∴
,∴![]() =
=![]() ,∴c=
,∴c=![]() b,a=
b,a=![]() =
=![]() b.
b.
∴![]() =
=![]() =
=![]() .
.
(2)直线l的斜率不为0时,设直线l的方程为:ty=x﹣1.设C(x1,y1),D(x2,y2).
联立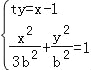 ,化为:(t2+3)y2+2ty+1﹣3b2=0,
,化为:(t2+3)y2+2ty+1﹣3b2=0,
y1+y2=![]() ,y1y2=
,y1y2=![]() ,
,
∵k1+k2=2,∴![]() +
+![]() =2,
=2,
化为:(y1﹣2)(ty2﹣2)+(y2﹣2)(ty1﹣2)=2(ty1﹣2)(ty2﹣2),
即:ty1y2=y1+y2,
∴t![]() =
=![]() ,对t∈R都成立.
,对t∈R都成立.
化为:b2=1,
直线l的斜率为0时也成立,
∴b2=1,
∴椭圆C的方程为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司生产电饭煲,每年需投入固定成本40万元,每生产1万件还需另投入16万元的变动成本,设该公司一年内共生产电饭煲
 万件并全部销售完,每一万件的销售收入为
万件并全部销售完,每一万件的销售收入为 万元,且
万元,且 (
( ),该公司在电饭煲的生产中所获年利润为
),该公司在电饭煲的生产中所获年利润为 (万元),(注:利润=销售收入-成本)
(万元),(注:利润=销售收入-成本)(1)写出年利润
 (万元)关于年产量
(万元)关于年产量 (万件)的函数解析式,并求年利润的最大值;
(万件)的函数解析式,并求年利润的最大值;(2)为了让年利润
 不低于2360万元,求年产量
不低于2360万元,求年产量 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】4月23日是“世界读书日”,某中学在此期间开展了一系列的读书教育活动,为了解本校学生课外阅读情况,学校随机抽取了100名学生对其课外阅读时间进行调查,下面是根据调查结果绘制的学生日均课外阅读时间(单位:分钟)的频率分布直方图,若将日均课外阅读时间不低于60分钟的学生称为“读书谜”,低于60分钟的学生称为“非读书谜”

(1)求
 的值并估计全校3000名学生中读书谜大概有多少?(将频率视为概率)
的值并估计全校3000名学生中读书谜大概有多少?(将频率视为概率) (2)根据已知条件完成下面2×2的列联表,并据此判断是否有99%的把握认为“读书谜”与性别有关?
非读书迷
读书迷
合计
男
15
女
45
合计
附:
 .
.
0.100
0.050
0.025
0.010
0.001

2.706
3.841
5.024
6.635
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,
中, ,
, ,
, ,平面
,平面 底面
底面 ,
, .
. 和
和 分别是
分别是 和
和 的中点,求证:
的中点,求证:
(Ⅰ)
 底面
底面 ;
;(Ⅱ)
 平面
平面 ;
;(Ⅲ)平面
 平面
平面 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
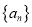 是公比为
是公比为 的等比数列,且
的等比数列,且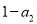 是
是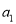 与
与 的等比中项,其前
的等比中项,其前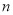 项和为
项和为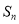 ;数列
;数列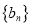 是等差数列,
是等差数列, 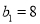 ,其前
,其前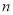 项和
项和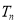 满足
满足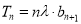 (
(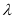 为常数,且
为常数,且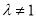 ).
).(1)求数列
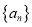 的通项公式及
的通项公式及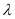 的值;
的值;(2)求
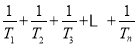 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】宝宝的健康成长是妈妈们最关心的问题,父母亲为婴儿选择什么品牌的奶粉一直以来都是育婴中的一个重要话题,为了解过程奶粉的知名度和消费者的信任度,某调查小组特别调查记录了某大型连锁超市2015年与2016年这两年销售量前5名的五个品牌奶粉的销量(单位:罐),绘制如下的管状图:
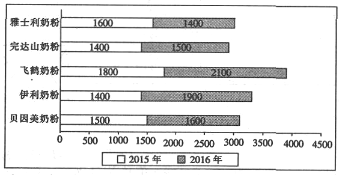
(1)根据给出的这两年销量的管状图,对该超市这两年品牌奶粉销量的前五强进行排名;
(2)分别计算这5个品牌奶粉2016年所占总销量(仅指这5个品牌奶粉的总销量)的百分比(百分数精确到各位),并将数据填入如下饼状图中的括号内;
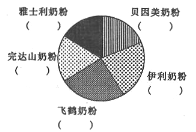
(3)试以(2)中的百分比作为概率,若随机选取2名购买这5个品牌中任意1个品牌的消费者进行采访,记
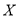 为被采访中购买飞鹤奶粉的人数,求
为被采访中购买飞鹤奶粉的人数,求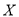 的分布列及数学期望.
的分布列及数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在各棱长均为4的直四棱柱
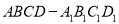 中,底面
中,底面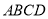 为菱形,
为菱形, 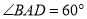 ,
, 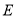 为棱
为棱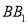 上一点,且
上一点,且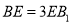 .
.(1)求证:平面
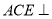 平面
平面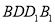 ;
;(2)求二面角
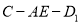 的正弦值.
的正弦值.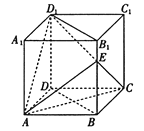
相关试题

