搜索
【题目】某班同学准备参加学校在寒假里组织的“社区服务”、“进敬老院”、“参观工厂”、“民俗调查”、“环保宣传”五个项目的社会实践活动，每天只安排一项活动，并要求在周一至周五内完成.其中“参观工厂”与“环保宣讲”两项活动必须安排在相邻两天，“民俗调查”活动不能安排在周一.则不同安排方法的种数是（ ）
A.48 B.24 C.36 D.64
参考答案：
【答案】C
【解析】
试题分析：当星期一排星期二参观工厂和环保宣讲活动时有
种，星期三至星期五可以随便安排剩下的活动有
种，共
种，当当星期一不排参观工厂或环保宣讲活动时，从社区服务或进敬老院中选一项活动来排星期一有
种，将参观工厂与环保宣讲两项活动捆绑在一起与剩下的2项活动排星期二至星期五共有
种，共
种，据分类计数原理知不同的安排方法共36种
-
科目： 来源： 题型：
查看答案和解析>>【题目】（本小题满分14分）
设△ABC三个内角A、B、C所对的边分别为a，b，c. 已知C＝
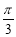，acosA=bcosB．（1）求角A的大小；
（2）如图，在△ABC的外角∠ACD内取一点P，使得PC＝2．过点P分别作直线CA、CD的垂线PM、PN，垂足分别是M、N．设∠PCA＝α，求PM＋PN的最大值及此时α的取值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】若
， 
， 
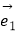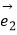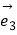为同一平面内互不共线的三个单位向量，并满足 + + = 
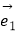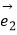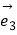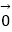，且向量 
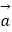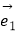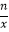
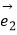=x + 
+（x+ 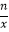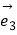） （x∈R，x≠0，n∈N+）．
（1）求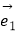 与 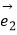所成角的大小；
（2）记f（x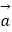）=| |，试求f（x）的单调区间及最小值． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知a＞0，设命题p：函数f（x）=x2﹣2ax+1﹣2a在区间[0，1]上与x轴有两个不同的交点；命题q：g（x）=|x﹣a|﹣ax有最小值．若（￢p）∧q是真命题，求实数a的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，正方形AA1D1D与矩形ABCD所在平面互相垂直，AB=2AD=2，点E为AB的中点．
（1）求证：BD1∥平面A1DE；
（2）求直线A1E与平面AD1E所成角． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知△ABC的三内角A，B，C所对的边分别是a，b，c，△ABC的面积S=
且sinA=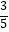 
．
（1）求sinB；
（2）若边c=5，求△ABC的面积S． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知椭圆C的两个焦点坐标分别是F1（﹣
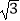，0）、F2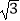（ ，0），并且经过点P（ ，﹣ 
）．
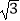（1）求椭圆C的方程；
（2）若直线l与圆O：x2+y2=1相切，并与椭圆C交于不同的两点A、B．当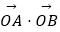
=λ，且满足 ≤λ≤ 
时，求△AOB面积S的取值范围．
相关试题
