【题目】商场销售某一品牌的羊毛衫,购买人数是每件羊毛衫标价的一次函数,标价越高,购买人数越少,把购买人数为零时的最低标价称为无效价格,已知无效价格为每件300元,已知这种羊毛衫的成本价是100元/件,商场以高于成本价的价格(标价)出售.求:
(1)商场要获取最大利润,羊毛衫的标价应定为每件多少元?
(2)通常情况下,获取最大利润只是一种“理想结果”,如果商场要获得最大利润的75%,那么羊毛衫的标价为每件多少元?
参考答案:
【答案】(1)商场要获取最大利润,羊毛衫的标价应定为每件![]() 元;(2)要获取最大利润的
元;(2)要获取最大利润的![]() ,每件标价为
,每件标价为![]() 元或
元或![]() 元.
元.
【解析】
试题分析:(1)设出函数的解析式,确定利润函数,利用配方法,即可求出最大利润和羊毛衫的标价;(2)利用商场要获得的最大利润的![]() ,建立方程,即可求得结论.
,建立方程,即可求得结论.
试题解析:(1)设购买人数为![]() 人,羊毛衫的标价为每件
人,羊毛衫的标价为每件![]() 元,利润为
元,利润为![]() 元,
元,
则![]() ,
,![]()
![]() ,
,
由题意,得![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]()
![]() (
(![]() ),
),
∵![]() ,
,
∴![]() 时,
时,![]() ,
,
即商场要获取最大利润,羊毛衫的标价应定为每件200元.
(2)解:由题意得![]() ,
,
![]() ,解得
,解得![]() 或
或![]() ,
,
所以,商场要获取最大利润的![]() ,每件标价为250元或150元.
,每件标价为250元或150元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于定义域为
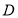 的函数
的函数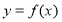 ,如果存在区间
,如果存在区间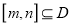 ,同时满足:
,同时满足:①
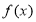 在
在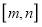 上是单调函数;
上是单调函数;②当定义域是
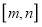 时,
时,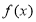 的值域也是
的值域也是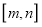 .
.则称
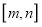 是该函数的“等域区间”.
是该函数的“等域区间”.(1)求证:函数
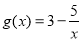 不存在“等域区间”;
不存在“等域区间”;(2)已知函数
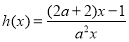 (
(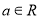 ,
,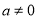 )有“等域区间”
)有“等域区间”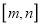 ,求实数
,求实数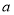 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标平面中,
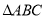 的两个顶点为
的两个顶点为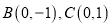 ,平面内两点
,平面内两点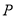 、
、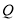 同时满足:①
同时满足:①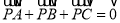 ;②
;②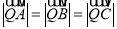 ;③
;③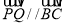 .
.(1)求顶点
 的轨迹
的轨迹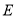 的方程;
的方程;(2)过点
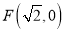 作两条互相垂直的直线
作两条互相垂直的直线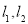 ,直线
,直线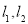 与点
与点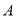 的轨迹
的轨迹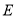 相交弦分别为
相交弦分别为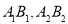 ,设弦
,设弦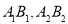 的中点分别为
的中点分别为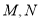 .
.①求四边形
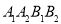 的面积
的面积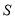 的最小值;
的最小值;②试问:直线
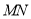 是否恒过一个定点?若过定点,请求出该定点,若不过定点,请说明理由.
是否恒过一个定点?若过定点,请求出该定点,若不过定点,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直三棱柱
 中,
中, ,
, ,点
,点 在线段
在线段 上.
上.
(1)若
 是
是 中点,证明:
中点,证明: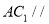 平面
平面 ;
;(2)当
 长是多少时,三棱锥
长是多少时,三棱锥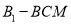 的体积是三棱柱
的体积是三棱柱 的体积的
的体积的 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的左右顶点为
的左右顶点为 、
、 ,左右焦点为
,左右焦点为 ,其长半轴的长等于焦距,点
,其长半轴的长等于焦距,点 是椭圆上的动点,
是椭圆上的动点, 面积的最大值为
面积的最大值为 .
.(1)求椭圆的方程;
(2)设
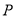 为直线
为直线 上不同于点
上不同于点 的任意一点,若直线
的任意一点,若直线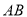 、
、 分别与椭圆交于异于
分别与椭圆交于异于 、
、 的点
的点 、
、 ,判断点
,判断点 与以
与以 为直径的圆的位置关系.
为直径的圆的位置关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】设命题p:x>0,x-lnx>0,则¬p为
A. x0>0,x0-lnx0>0 B. x0>0,x0-lnx0≤0
C. x>0,x-lnx<0 D. x>0,x-lnx≤0
-
科目: 来源: 题型:
查看答案和解析>>【题目】圆x2+y2-4x+6y=0和圆x2+y2-6x=0交于A,B两点,则直线AB的方程是( )
A. x+y+3=0 B. 3x-y-9=0
C. x+3y=0 D. 4x-3y+7=0
相关试题

