【题目】已知函数f(x)= ![]() +x,x∈[3,5].
+x,x∈[3,5].
(1)判断函数f(x)的单调性,并利用单调性定义证明;
(2)求函数f(x)的最大值和最小值.
参考答案:
【答案】
(1)证明:设任意变量x1,x2且3<x1<x2<5
f(x1)﹣f(x2)= ![]()
= ![]()
= ![]() ;
;
∵3<x1<x2<5
∴x1x2>0,x2﹣x1>0,1﹣x1x2<0;
∴f(x1)<f(x2);
∴函数f(x)为x∈[3,5]增函数
(2)解:由(1)知函数f(x)为x∈[3,5]增函数;
∴ ![]()
【解析】(1)根据函数单调性定义证明f(x)的单调性;(2)根据函数的增减性来求特定区间上的最值问题;
【考点精析】掌握利用导数研究函数的单调性和函数的最大(小)值与导数是解答本题的根本,需要知道一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)(x∈R)为奇函数,f(1)=
 ,f(x+2)=f(x)+f(2),则f(5)=( )
,f(x+2)=f(x)+f(2),则f(5)=( )
A.0
B.1
C.
D.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2﹣2x,g(x)=ax+2(a>0),且对任意的x1∈[﹣1,2],都存在x2∈[﹣1,2],使f(x2)=g(x1),则实数a的取值范围是( )
A.[3,+∞)
B.(0,3]
C.[ ,3]
,3]
D.(0, ]
] -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知长方形
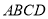 中,
中,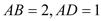 ,
, 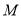 为
为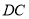 的中点。将
的中点。将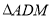 沿
沿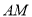 折起,使得平面
折起,使得平面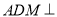 平面
平面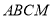 。
。(1)求证:
 ;
; (2)若点
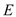 是线段
是线段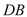 上的一动点,问点E在何位置时,二面角
上的一动点,问点E在何位置时,二面角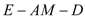 的余弦值为
的余弦值为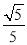 。
。
-
科目: 来源: 题型:
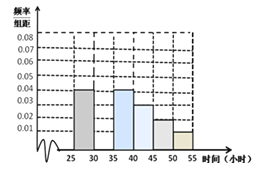
查看答案和解析>>【题目】教育部,体育总局和共青团中央号召全国各级各类学校要广泛,深入地开展全国亿万大,中学生阳光体育运动,为此,某校学生会对高二年级2014年9月与10月这两个月内参加体育运动的情况进行统计,随机抽取了100名学生作为样本,得到这100名学生在该月参加体育运动总时间的小时数,根据此数据作出了如下的频数和频率的统计表和 频率分布直方图:
(I)求a,p的值,并补全频率分布直方图;
(Ⅱ)根据上述数据和直方图,试估计运动时间在[25,55]小时的学生体育运动的平均时间;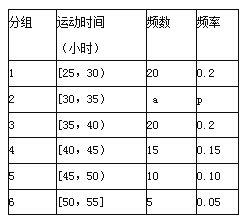
-
科目: 来源: 题型:
查看答案和解析>>【题目】集合P={x|a+1≤x≤2a+1},Q={x|﹣2≤x≤5}
(1)若a=3,求集合(RP)∩Q;
(2)若PQ,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】(选修4—4;坐标系与参数方程)已知曲线
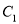 的极坐标方程是
的极坐标方程是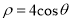 ,曲线
,曲线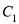 经过平移变换
经过平移变换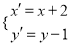 得到曲线
得到曲线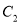 ;以极点为原点,极轴为
;以极点为原点,极轴为 轴正方向建立平面直角坐标系,直线l的参数方程是
轴正方向建立平面直角坐标系,直线l的参数方程是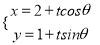 (
(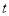 为参数).
为参数).(1)求曲线
 ,
, 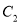 的直角坐标方程;
的直角坐标方程;(2)设直线l与曲线
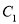 交于
交于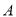 、
、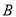 两点,点
两点,点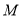 的直角坐标为(2,1),若
的直角坐标为(2,1),若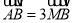 ,求直线l的普通方程.
,求直线l的普通方程.
相关试题

