【题目】大学生赵敏利用寒假参加社会实践,对机械销售公司7月份至12月份销售某种机械配件的销售量及销售单价进行了调查,销售单价![]() 和销售量
和销售量![]() 之间的一组数据如下表所示:
之间的一组数据如下表所示:
月份 | 7 | 8 | 9 | 10 | 11 | 12 |
销售单价 | 9 | 9.5 | 10 | 10.5 | 11 | 8 |
销售量 | 11 | 10 | 8 | 6 | 5 | 14 |
(1)根据7至11月份的数据,求出![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差不超过0.5元,则认为所得到的回归直线方程是理想的,试问(1)中所得到的回归直线方程是否理想?
(3)预计在今后的销售中,销售量与销售单价仍然服从(1)中的关系,若该种机器配件的成本是2.5元/件,那么该配件的销售单价应定为多少元才能获得最大利润?(注:利润=销售收入-成本).
参考公式:回归直线方程![]() ,其中
,其中 ,参考数据:
,参考数据: ![]() .
.
参考答案:
【答案】(1)![]() (2)可以认为所得到的回归直线方程是理想的(3)产品的销售单价定为7.5元/件时,获得的利润最大.
(2)可以认为所得到的回归直线方程是理想的(3)产品的销售单价定为7.5元/件时,获得的利润最大.
【解析】试题分析:(1)根据回归直线方程公式,求![]() ,则
,则![]() ,即可;(2)利用回归直线方程,估测
,即可;(2)利用回归直线方程,估测![]() 时,
时, ![]() ,计算误差确定是理想拟合;(3)写出销售利润
,计算误差确定是理想拟合;(3)写出销售利润![]() ,利用均值不等式求最大值.
,利用均值不等式求最大值.
试题解析:(1)因为![]() ,
,
所以![]() ,则
,则![]() ,
,
于是![]() 关于
关于![]() 的回归直线方程为
的回归直线方程为![]() ;
;
(2)当![]() 时,
时, ![]() ,则
,则![]() ,
,
所以可以认为所得到的回归直线方程是理想的;
(3)令销售利润为![]() ,则
,则![]() ,
,
因为![]() ,
,
当且仅当![]() ,即
,即![]() 时,
时, ![]() 取最大值.
取最大值.
所以该产品的销售单价定为7.5元/件时,获得的利润最大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在正方体ABCD﹣A1B1C1D1中,点M是平面A1B1C1D1内一点,且BM∥平面ACD1 , 则tan∠DMD1的最大值为( )

A.
B.1
C.2
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在边长为3的正三角形中,
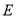 ,
, 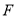 ,
, 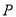 分别为
分别为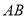 ,
, 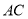 ,
, 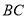 上的点,且满足
上的点,且满足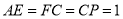 .将
.将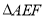 沿
沿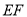 折起到
折起到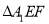 的位置,使平面
的位置,使平面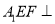 平面
平面 ,连结
,连结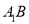 ,
,  ,
, 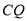 .(如图2)
.(如图2)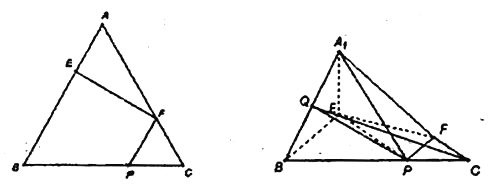
(Ⅰ)若
 为
为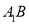 中点,求证:
中点,求证: 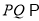 平面
平面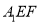 ;
;(Ⅱ)求证:
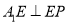 ;
;(Ⅲ)求
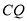 与平面
与平面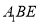 所成角的正切.
所成角的正切. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知单调递增的等比数列
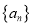 满足
满足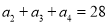 ,且
,且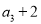 是
是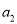 ,
, 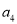 的等差中项.
的等差中项.(Ⅰ)求数列
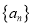 的通项公式;
的通项公式;(Ⅱ)若数列
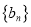 满足
满足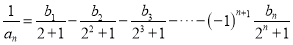 ,求数列
,求数列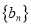 的通项公式;
的通项公式;(Ⅲ)在(Ⅱ)的条件下,设
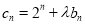 ,问是否存在实数
,问是否存在实数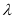 使得数列
使得数列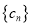 (
(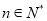 )是单调递增数列?若存在,求出
)是单调递增数列?若存在,求出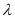 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}满足:a1=m(m为正整数),an+1=
 若a6=1,则m所有可能的取值的个数为 .
若a6=1,则m所有可能的取值的个数为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】下面给出四个命题的表述: ①直线(3+m)x+4y﹣3+3m=0(m∈R)恒过定点(﹣3,3);
②线段AB的端点B的坐标是(3,4),A在圆x2+y2=4上运动,则线段AB的中点M的轨迹方程 +(y﹣2)2=1
+(y﹣2)2=1
③已知M={(x,y)|y=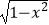 },N={(x,y)|y=x+b},若M∩N≠,则b∈[﹣
},N={(x,y)|y=x+b},若M∩N≠,则b∈[﹣ 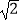 ,
, 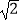 ];
];
④已知圆C:(x﹣b)2+(y﹣c)2=a2(a>0,b>0,c>0)与x轴相交,与y轴相离,则直线ax+by+c=0与直线x+y+1=0的交点在第二象限.
其中表述正确的是( (填上所有正确结论对应的序号) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形ABC的顶点坐标为A(﹣1,5)、B(﹣2,﹣1)、C(4,3).
(1)求AB边上的高线所在的直线方程;
(2)求三角形ABC的面积.
相关试题

