搜索
)＞f(2a-1)，求实数a的取值范围.
参考答案：
解析：本题的解题关键是如何使用已知条件f()＞f(2a-1)，即如何把这个已知条件转化成关于a的不等式，也就是把自变量“部分”要化到一个单调区间内，才能根据函数的单调性达到转化的目的.这时我们想到了“若f(x)是偶函数，那么f(x)=f(-x)=f(|x|).”于是f(2a-1)=f(|2a-1|).
解：由f(x)是偶函数,且f(
)＞f(2a-1)等价于f(
)＞f(|2a-1|)，又f(x)在［0,+∞)上是减函数，
∴
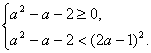
解得a≤-1或a≥2.
-
科目： 来源： 题型：
查看答案和解析>>下列结论中正确的是①②③①②③．
①函数y=f（x）是定义在R上的偶函数，且f（x+1）=-f（x），则函数y=f（x）的图象关于直线x=1对称；
②已知ξ～N（16，σ2），若P（ξ＞17）=0.35，则P（15＜ξ＜16）=0.15；
③已知f(x)是定义在(-∞，+∞)上的偶函数，且在(-∞，0]上是增函数．设a=f(ln
)，b=f(log43)，1 3 c=f(0.4-1.2)，则c＜a＜b；
④线性相关系数r的绝对值越接近于1，表明两个变量线性相关程度越弱． -
科目： 来源： 题型：
已知f(x)是定义在实数集R上的函数,它的反函数为f-1(x),若y=f-1(x+1)与y=f(x+1)互为反函数,且f(1)=1,则f(2)的值为查看答案和解析>>A.2 B.1 C.0 D.-1
-
科目： 来源： 题型：
查看答案和解析>>已知f(x)是定义在R上的不恒为零的函数，且对于任意的a,b∈R,满足f(a·b)=af(b)+bf(a),f(2)=2,a
=
(n∈N*),b=
(n∈N*);考查下列结论：①f(0)=f(1);②f(x)为偶函数；③数列{a
}为等比数列；④{b}为等差数列.其中正确的是 .
-
科目： 来源：2015届广东省高一第一次阶段考试数学试卷（解析版） 题型：解答题
查看答案和解析>>（本小题满分14分）已知f(x)是定义在( 0，＋∞)上的增函数，
且f(
) =
f(x)－f(y) （1）求f(1)的值;
（2）若f(6)= 1，解不等式 f( x＋3 )－f(
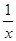) ＜2 -
科目： 来源：2010年黑龙江省高一上学期期末考试数学试卷 题型：填空题
查看答案和解析>>已知f (x)是定义在
∪
上的奇函数，当
时，f (x)的图象如图所示，那么f (x)的值域是
相关试题
